

Depuis 2004, chaque année, j'anime auprès de L'Institut Européen des Arts Céramiques de Guebwiller un stage sur les émaux de haute température.
Les élèves de l'IEAC reçoivent une formation sur une année entière donnée par des professeurs permanents. Mais à cette formation viennent s'ajouter quelques stages « événements » assurés par des intervenants ponctuels. Ces stages sont ouverts et donc proposés à des candidatures externes. Dates des stages et tarifs des formations sont indiqués en temps voulu sur le site de l'IEAC.
La formation que j'assure dure cinq journées et s'appuie sur le document ci-dessous. Un grand merci à frère Daniel de Montmollin pour son autorisation à reproduire et utiliser certains de ses diagrammes.
Une glaçure de grès (on peut aussi parler d’émail ou de couverte) est une variété de verre. Dans ce cas précis, on parle aussi de silicate, ce qui donne déjà une indication essentielle sur l’élément principal de ce verre : la silice. Mais si cet émail n’était composé que de silice, il faudrait atteindre une température proche de 1700 °C pour obtenir sa fusion. Aucune argile à grès ne supporterait une telle température.
On ajoutera donc à cette silice d’autres éléments, oxydes divers fournis par les minéraux pour abaisser ce point de fusion et obtenir un émail à une température exploitable de grésage de l’argile, en gros de 1200 °C à 1300 °C (nous reviendrons plus loin sur la notion d’eutexie).
Bien que l’émail soit un verre véritable, il lui faudra encore une qualité propre qui le différencie des verres utilisés par les verriers. En effet, fondu, il devra adhérer à son support d’argile et ne pas se répandre comme de l’eau sur la plaque d’enfournement. Il lui faudra avoir à un haut degré cette qualité que l’on nomme «viscosité». C’est l’alumine qui assurera cette fonction.
On voit déjà se dessiner trois groupes distincts dans la composition d’une glaçure :
Nous allons reprendre en détail les différents éléments formant les glaçures en les classant pour former les trois colonnes qui donnent la formule unité de l’émail. Cette formule unité est aussi nommée formule de Seger.
Ces minéraux qui permettent d’abaisser le point de fusion de la silice (et dont nous verrons plus loin ce qu’ils sont) apportent plus précisément dans l’émail un certain nombre d’oxydes que l’on nomme «basiques». Ce sont :
Ayant des fonctions proches dans la fusion de l’émail et étant souvent associés dans un même minéral, les oxydes de potassium et de sodium sont généralement réunis dans la formule unité sous l’appellation KNaO.
Il est sans doute bon d’ouvrir une parenthèse pour expliquer en quelques lignes la notion de mole et de masse molaire. L’échelle atomique n’est pas adaptée aux travaux des chimistes et accessoirement aux recherches des céramistes. Il faut donc travailler sur un groupe d’atomes tel que sa masse soit à notre échelle. Cet ensemble s’appelle une mole et il est formé de 6,02 × 1023 atomes : c’est la constante d’Avogadro.
Imaginez le nombre 602 suivi de 21 zéros, ou encore «600 mille milliards de milliards» d’atomes. Dans l’exemple de l’atome de silicium, Si, la somme des masses de cet ensemble d’atomes me donne 28 g de matière. 28 est donc la masse molaire de Si. Pour l’atome d’oxygène, O, j’obtiens une masse molaire de 16. Pour calculer la masse molaire de la molécule, il suffit de faire la somme des masses molaires des atomes qui la composent. Dans l’exemple de la silice, SiO2, j’obtiens bien une masse molaire égale à 28 + (16 × 2) = 60.
La formule unité d’un émail nous donne donc les rapports molaires des oxydes les uns par rapport aux autres. Pour faciliter les comparaisons entre différentes glaçures, on admettra par convention que le total de la première colonne est toujours égal à 1. C’est à cette première colonne regroupant les oxydes basiques que l’on donnera le nom de «mole basique».
C’est en faisant varier les trois oxydes de cette mole basique, c’est-à-dire : CaO, MgO et KNaO que Daniel de Montmollin a établi les 60 diagrammes pour 60 moles basiques différentes qui composent son ouvrage : «Pratique des émaux 1300 °C».
Toutes les combinaisons possibles entre CaO, MgO et KNaO dans une progression de 0,1 en 0,1 sont représentées sous forme de triangle. C’est un exemple de ce que l’on appelle un mélange ternaire.
Les sommets sont formés d’une mole entière de l’oxyde retenu. La mole basique du diagramme n°1 est formée seulement de CaO. De même, KNaO compose seul la mole basique du diagramme n°60. Par contre, il n’y a pas de sommet MgO car un émail dont la mole basique serait formée du seul oxyde de magnésium ne fondrait pas à température du grès car trop réfractaire. C’est pour cette même raison que cinq autres diagrammes proches de ce sommet n’ont pas été retenus (on y reviendra en abordant la notion d’eutexie).
La base opposée à chacun des sommets ne contient pas l’oxyde qui compose la totalité de la mole basique de ce sommet. La rangée suivante en contient 0,1 puis celle du dessus 0,2 et ainsi de suite jusqu’au sommet par une progression de 0,1 mole en 0,1 mole.
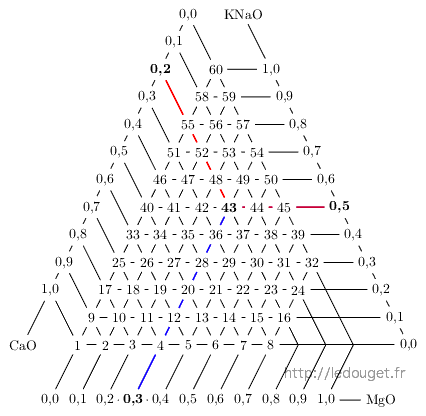
Figure 1.1: Le triangle des 60 diagrammes.
la mole du diagramme n°43 sera donc composée de
Les côtés du triangle du mélange ternaire représentent donc les diagrammes dont les moles basiques sont formées de deux oxydes. A l’intérieur du triangle, nous trouvons les diagrammes dont les moles basiques sont formées du mélange des trois oxydes.
Pour chacune de ces 60 moles basiques retenues, Daniel de Montmollin a établi un diagramme de fusion.
Voici comment se présente un diagramme de fusion. L’exemple retenu est le n°1, celui dont la mole basique est formée en totalité d’oxyde de calcium, CaO.
Le diagramme indique les rapports entre l’alumine, l’oxyde amphotère classé en colonne 2 et la silice, l’oxyde acide de la colonne 3.
En abscisse, (axe horizontal) nous avons la progression d’alumine, Al2O3 de 0,05 en 0,05 mole. En ordonnée, (axe vertical) nous avons la progression de silice, SiO2 de 0,5 en 0,5 mole.
Le tracé représenté définit la zone de fusion possible et exploitable pour un émail de grès cuit de 1280 à 1300 °C. Ce tracé a été établi à partir d’un point eutectique.
C’est le moment de définir ce qu’est la notion d’eutexie.
L’eutexie est la température de fusion d’un mélange chimique fondant à température constante inférieure au point de fusion de chacun des constituants. Dans le cas du diagramme choisi, le n°1, il s’agit du point de fusion le plus bas obtenu en associant d’une manière précise et définie les trois éléments retenus, CaO, Al2O3 et SiO2.
Rappelons d’abord que pris séparément :
Le point eutectique de ce diagramme connu sous le nom d’«eutectique chaux» correspond à la formule suivante : CaO 0,35 Al2O3 2,48 SiO2. Son point de fusion est à 1170 °C.
Si on positionne ce point sur le diagramme, on voit qu’il est centré dans la zone définie par Daniel de Montmollin. Il faut donc s’éloigner de ce point eutectique d’une certaine distance pour obtenir un émail qui fonde à la température choisie de 1280 ou 1300 °C. Trop près du point eutectique, l’émail sera trop fusible ; trop éloigné, il ne fondra pas suffisamment.
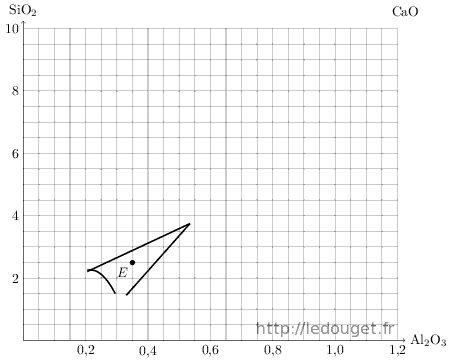
Figure 1.2: Diagramme n°1.
C’est une autre eutectique qui nous explique pourquoi six diagrammes n’ont pas pu être établis du côté du sommet MgO : MgO 0,39 Al2O3 2 SiO2 en effet ne fond pas en-dessous de 1350 °C.
Ce petit tracé sur ce diagramme de fusion est riche d’enseignement car il permet du même coup de comprendre que la notion généralement admise qui consiste à distinguer entre éléments «fondants» et éléments «réfractaires» de l’émail ne tient pas.
En effet, imaginons une glaçure de départ située en dessous du point eutectique. En ajoutant à cette glaçure une certaine quantité de silice, on peut donc s’approcher du point eutectique et rendre la glaçure plus fusible. Dans ce cas précis, on pourra donc attribuer à la silice un rôle de fondant. Cependant si on ajoute une quantité de silice telle qu’on dépasse ce point eutectique et qu’on s’en éloigne suffisamment pour que la glaçure devienne infusible, on pourra dire alors au contraire que la silice est cette fois un élément réfractaire.
On peut faire la même démonstration avec l’alumine ou avec l’oxyde de calcium suivant que l’on s’approche ou que l’on s’éloigne de ce point eutectique et affirmer ainsi que chaque élément de l’émail peut donc favoriser ou non la fusion de l’ensemble.
Pour revenir au tracé proposé par Daniel de Montmollin, théoriquement la fusion de l’émail se fera à 1280 °C si on se tient à la limite de la zone définie. On remarque que le tracé est interrompu à 1,5 moles de silice car en effet au-dessous de ce seuil, on considère que l’émail ne serait pas suffisamment stable, ni assez résistant à l’abrasion.
Mais avant même de pouvoir commencer à utiliser ces diagrammes de fusion, il faudra se demander quelles sont les matières premières qui vont nous permettre de fournir tous ces oxydes qui composent les trois colonnes de notre formule unité.
L’oxyde de calcium sera fourni par le carbonate de chaux dont la formule est CaCO3 et la masse molaire 100.
On trouve dans les manuels céramiques les termes de «chaux», «craie» ou «blanc d’Espagne» qui désignent tous la même matière.
L’oxyde de magnésium sera fourni par le talc (appelé aussi stéatite). En plus d’apporter l’oxyde de magnésium, le talc fournira de l’alumine en petite quantité et de la silice. Voici un talc fourni par Céradel Socor et dont j’ai calculé la formule : MgO 0,12 Al2O3 SiO2 pour une masse molaire de 126.
Mais il est possible d’apporter MgO dans une glaçure en utilisant d’autres matières premières comme le carbonate de magnésium ou magnésite, MgCO3 dont la masse molaire est 84, mais aussi la dolomie qui en plus de l’oxyde de magnésium nous fournira une quantité à peu près égale d’oxyde de calcium. Sa formule théorique est CaCO3 MgCO3 pour une masse molaire de 184.
Les oxydes de sodium et de potassium sont apportés dans l’émail par les feldspaths essentiellement. Ceux-ci seront plutôt potassiques ou plutôt sodiques mais toujours assez éloignés dans leur composition des formules théoriques fournies par les manuels de chimie.
Nous retiendrons essentiellement l’orthose ou feldspath potassique dont la formule théorique est : K2O Al2O3 6 SiO2 et l’albite ou feldspath sodique dont la formule est : Na2O Al2O3 6 SiO2.
Nous verrons plus loin comment établir la véritable formule d’un feldspath à partir de son analyse chimique établie en pourcentage de chacun de ses composants.
Un autre «feldspathoïde» se révélera également intéressant à l’usage. Il s’agit de la syénite néphéline dont la particularité est d’avoir une teneur moindre en silice que les autres feldspaths.
Nous avons déjà rencontré plus haut deux matières premières qui nous fournissent en plus des oxydes basiques recherchés, une certaine quantité d’alumine. C’est vrai pour le talc dans une faible proportion mais surtout pour les feldspaths qui possèdent dans leur formule une mole et souvent plus d’alumine.
Mais le fournisseur attitré d’alumine dans une glaçure sera le kaolin :
Nous avons aussi vu précédemment trois matières premières qui nous apportent de la silice : le talc, le feldspath et le kaolin. Le complément nécessaire à une glaçure se fera par le quartz broyé qui est une forme de silice pure : SiO2 dont la masse molaire est 60.
La plupart des matériaux fournis par la nature n’ont pas une composition correspondant exactement à la formule théorique établie par les minéralogistes.
Il sera donc intéressant d’établir la formule véritable des matériaux choisis, à condition toutefois de disposer des analyses chimiques fournies par les marchands. Ces analyses indiquent les pourcentages réels des divers oxydes présents dans la matière première.
Nous allons prendre dans le catalogue Céradel Socor l’analyse fournie pour le feldspath potassique pour en calculer sa formule moléculaire et sa masse molaire véritables. Nous verrons alors que nous sommes assez loin de la formule théorique : K2O Al2O3 6 SiO2.
L’analyse suivante est fournie :
| SiO2 | 68,20 % |
| Al2O3 | 18,00 % |
| K2O | 10,50 % |
| Na2O | 2,70 % |
| CaO | 0,20 % |
| MgO | 0,15 % |
| Fe2O3 | 0,12 % |
| TiO2 | 0,02 % |
| Total | 99,89 % |
On ne retiendra pour le calcul que les oxydes présents en quantité significative, ce qui ne veut pas dire que les éléments même en faible quantité n’auront pas leur rôle à jouer dans l’émail.
On va diviser l’ensemble des oxydes présents dans cette analyse par leurs masses molaires respectives :
| SiO2 | 68,20 % | divisé par | 60 | nous donne | 1,1366 | moles |
| Al2O3 | 18,00 % | — | 102 | — | 0,1764 | — |
| K2O | 10,50 % | — | 94 | — | 0,1117 | — |
| Na2O | 2,70 % | — | 62 | — | 0,0435 | — |
Comme pour la formule unité d’un émail, on range les oxydes en trois colonnes (basique, amphotère et acide) pour une première formule provisoire :
| K2O | 0,1117 | Al2O3 | 0,1764 | SiO2 | 1,1366 |
| Na2O | 0,0435 | ||||
| 0,1552 |
En ramenant la mole basique à 1 on obtient la formule définitive du feldspath. Il suffit pour cela de diviser toutes les valeurs par 0,1552 :
| K2O | 0,72 | Al2O3 | 1,1366 | SiO2 | 7,3234 |
| Na2O | 0,28 |
Ou en simplifiant : KNaO Al2O3 1,14 SiO2 7,32.
À comparer avec la formule théorique : K2O Al2O3 SiO2 6
En notant également qu’un feldspath dit «potassique» affiche en réalité une part sodique supérieure à 25 % de la mole basique.
La masse molaire de ce feldspath peut ensuite être calculée comme suit :
| Quantité moléculaire | m.m. | |||
| 0,72 K2O | × | 94 | = | 67,68 |
| 0,28 Na2O | × | 62 | = | 17,36 |
| 1,14 Al2O3 | × | 102 | = | 116,28 |
| 7,3 SiO2 | × | 60 | = | 438,00 |
| 639,32 |
Mais il faudrait en réalité y ajouter aussi les masses des éléments non retenus pour la formule parce qu’en quantités trop faibles : CaO, MgO, Fe2O3, TiO2. On peut beaucoup plus simplement obtenir un résultat plus juste en divisant le total des oxydes de l’analyse fournie par le même diviseur, celui qui nous a permis de passer de la formule provisoire à la formule définitive : 0,1552. Le total de l’analyse, soit 99,89 %, divisé par 0,1552 nous donne une masse molaire de 643.
Une fois définies les formules moléculaires et les masses molaires des matériaux retenus, il sera possible de s’attaquer alors à la réalisation des premières glaçures.
Choisissons au hasard dans le diagramme n°1 une formule d’émail qui pourrait être la suivante : CaO 0,6 Al2O3 4 SiO2. Il est bien évident que dans ce diagramme, la mole basique sera toujours CaO et que seules les quantités d’alumine et de silice peuvent varier
Comment parvenir à une recette exploitable à partir de cette formule unité ?
C’est le carbonate de chaux qui va me fournir la totalité de CaO soit une mole de carbonate de chaux qui me donnera une mole de CaO. Dans le tableau j’inscris donc 1 à la suite de carbonate de chaux et 1/0 dans la colonne réservée à CaO ce qui signifie : «1 fourni, reste à fournir 0».
C’est le kaolin qui va me donner toute l’alumine demandée dans la formule retenue soit 0,6. Je prendrai donc 0,6 mole de kaolin qui va me donner 0,6 mole d’Al2O3 mais aussi et forcément une part de silice qu’il est facile de calculer : 0,6 × 2 SiO2 = 1,2 SiO2. Rappelons en effet que la formule du kaolin est : Al2O3 2 SiO2 2 H2O
On ne tient pas compte de l’eau de constitution qui quittera la glaçure sous forme de vapeur.
J’inscris donc 0,6/0 dans la colonne Al2O3 car toute l’alumine a été fournie et 1,2/2,8 dans la colonne SiO2 car en effet il reste à fournir 2,8 SiO2 pour arriver aux 4 SiO2 demandés dans la formule unité de l’émail retenu.
Les 2,8 SiO2 manquant me seront apportés par de la silice pure sous forme de quartz broyé : d’où Quartz 2,8 et 2,8/0 dans la colonne SiO2.
La recette est désormais complète et on peut la faire figurer et la visionner clairement dans un tableau (cf. tableau 1.1).
CaO Al2O3 0,6 SiO2 4 Chaux 1 1/0 Kaolin 0,6 0,6/0 1,2/2,8 Quartz 2,8 2,8/0
Tableau 1.1: La recette molaire.
Il faut maintenant multiplier la quantité molaire de chacune des matières premières par la masse molaire de celle-ci pour obtenir une recette en poids.
| Carbonate de chaux | 1,0 × 100 | = | 100,0 |
| Kaolin | 0,6 × 258 | = | 154,8 |
| Quartz | 2,8 × 60 | = | 168,0 |
Puis une simple règle de trois nous permettra de transformer cette recette en pourcentage :
| Carbonate de chaux | 100 | : | 422,8 × 100 | = | 23,65 |
| Kaolin | 154,8 | : | 422,8 × 100 | = | 36,61 |
| Quartz | 168 | : | 422,8 × 100 | = | 39,74 |
| 422,8 | 100,00 |
La recette composée de 23,65 g de carbonate de chaux, 36,61 g de kaolin et 39,74 g de quartz correspond donc à la formule unité du diagramme n°1 : CaO 0,6 Al2O3 4 SiO2.
Le principe reste le même mais cette fois-ci, il me faudra bien plus de matières premières pour me fournir l’ensemble des oxydes basiques. Prenons par exemple dans le diagramme n°43 la formule unité suivante :
| 0,2 | CaO | 0,9 | Al2O3 | 8 | SiO2 |
| 0,3 | MgO | ||||
| 0,5 | KNaO |
0,2 carbonate de chaux va me fournir la totalité de CaO, d’où dans le tableau, dans la colonne CaO : 0,2/0 (0,2 fourni, reste à fournir 0).
0,3 talc va me fournir tout MgO demandé soit 0,3 mais le talc m’apporte aussi de l’alumine et de la silice. Rappelons la formule retenue : MgO 0,12 Al2O3 SiO2. Il va donc me fournir aussi 0,3 × 0,12 = 0,036 Al2O3 et 0,3 SiO2 d’où dans le tableau :
Nous prendrons ensuite le feldspath potassique dont nous avons calculé précédemment la formule. Je la rappelle : KNaO 1,14 Al2O3 7,32 SiO2 masse molaire : 643. Il va nous fournir l’intégralité de KNaO soit 0,5 demandé mais aussi une partie de l’alumine soit 0,5 × 1,14 = 0,57 et une partie de la silice : 0,5 × 7,32 = 3,66.
Dans notre tableau nous aurons donc :
Le kaolin va me fournir ce qui manque encore en alumine pour atteindre les 0,9 Al2O3 demandés, soit 0,294. La formule de mon kaolin étant Al2O3 2 SiO2 il me donnera aussi 2 × 0,294 = 0,588 SiO2.
Nous aurons donc dans le tableau :
Il ne reste qu’à compléter par du quartz l’apport nécessaire pour atteindre les 8 SiO2 demandés par la formule choisie, soit 3,452 SiO2. Dans le tableau : 3,452/0 dans la colonne SiO2 (3,452 fourni, reste à fournir 0).
Dans la pratique, tous les calculs et démonstrations qui précèdent se noteront directement et de façon bien plus lisible dans le tableau 1.2.
CaO 0,2 MgO 0,3 KNaO 0,5 Al2O3 0,9 SiO2 8 Chaux 0,2 0,2/0 Talc 0,3 0,3/0 0,036/0,864 0,3/7,7 Feldspath 0,5 0,5/0 0,57/0,294 3,66/4,04 Kaolin 0,294 0,294/0 0,588/3,452 Quartz 3,452 3,452/0
Tableau 1.2: Tableau de la recette contenant trois oxydes basiques.
La recette pondérale qui correspond à cette formule du diagramme n°43 se calculera de la façon suivante :
| Carbonate de chaux | 0,2 | × | 100 | = | 20 |
| Talc | 0,3 | × | 126 | = | 37,8 |
| Feldspath potassique | 0,5 | × | 643 | = | 321,5 |
| Kaolin | 0,294 | × | 258 | = | 75,85 |
| Quartz | 3,452 | × | 60 | = | 207,12 |
| 662,27 |
Pour avoir la recette en pourcentage, une simple règle de trois suffit :
| Carbonate de chaux | 20,00 | : | 662,27 × 100 | = | 3,0 |
| Talc | 37,80 | : | 662,27 × 100 | = | 5,7 |
| Feldspath potassique | 321,50 | : | 662,27 × 100 | = | 48,5 |
| Kaolin | 75,95 | : | 662,27 × 100 | = | 11,5 |
| Quartz | 207,12 | : | 662,27 × 100 | = | 31,3 |
| 662,27 | 100,0 |
Avec un peu d’habitude, les mécanismes de calcul sont vite assimilés car la démarche est logique et relativement simple même si elle devient plus fastidieuse avec la multiplication des matières premières dans les recettes les plus élaborées.
Ces deux exemples ne représentent pourtant qu’une infime partie des possibilités qui s’ouvrent au céramiste devant les 60 diagrammes proposés par Daniel de Montmollin, chacun de ces diagrammes autorisant lui-même des centaines d’essais différents.
On est alors saisi de vertige car à défaut de pouvoir matériellement tout faire, que faudra-t-il choisir, quel diagramme retenir ? Et dans celui-ci, faudra-t-il calculer toutes les recettes possibles ? Cela demanderait un temps infini et même l’apport d’un logiciel informatique ne changerait rien quant au temps nécessaire à la réalisation des multiples pesées, à l’émaillage des plaquettes à essai et enfin à leur cuisson.
Nous allons voir qu’il est possible de se simplifier la tâche à différents niveaux de cette recherche. La première solution que je propose est de faire un choix limité mais judicieux des matières premières.
Quatre matières premières vont s’imposer en priorité et par là même nous indiquer les diagrammes qui nous seront les plus facilement accessibles. Ceux-ci nous permettront d’élaborer les recettes les plus simples car nécessitant moins de matériaux que d’autres, donc moins de calculs et de pesées. Il est faux de croire qu’une recette complexe nous donnerait forcément une glaçure plus intéressante qu’une recette simple. Les anciens Chinois nous ont prouvé le contraire.
Utilisées parfois seules ou associées deux à deux, ces matières premières vont nous permettre d’accéder à toutes les grandes familles «classiques» des émaux de haute température. Voici regroupés les diagrammes du mélange ternaire CaO, KNaO, MgO et les tracés indiquant les zones favorables au développement de tel ou tel type de glaçure.
Employés seuls, ils constituent déjà une glaçure. Si vous connaissez leur formule ou si vous êtes à même de la calculer à partir d’une analyse chimique comme nous l’avons fait précédemment, vous voyez que vous avez toutes les données nécessaires pour les positionner précisément dans le diagramme n°60. En effet, la mole basique d’un feldspath est bien KNaO et la suite de sa formule nous indique les quantités molaires d’Al2O3 et de SiO2.
Nous sommes au cœur d’une zone favorable à cette famille de glaçures que les Japonais nomment «Shino».
Seule pour former la mole basique, elle nous fait entrer dans le diagramme n°1 ; c’est le diagramme qui permet entre autres de développer le «céladon» calcique. A nous de trouver les meilleurs apports en alumine et en silice, sans oublier une petite quantité de fer, pour en obtenir la plus belle qualité.
Si maintenant nous associons Feldspath et chaux dans tous les rapports possibles de la mole basique KNaO-CaO, nous allons nous déplacer sur l’arête du triangle et passer par tous les diagrammes entre les sommets 1 et 60, soit les n°9-17-25-33-40-46-51-55-58.
Au passage, notons que la zone des diagrammes 25 et 33 est très polyvalente et qu’elle nous permettra de réaliser tout aussi bien des céladons, des bleus de fer que des «temmoku» ou noirs de fer.
La dolomie fournit en quantités théoriquement égales CaO et MgO. Employée seule pour fournir la mole basique, elle nous fait donc accéder au diagramme n°6, à mi-distance entre les sommets CaO et MgO.
Associée à un feldspath, elle va nous permettre de traverser le triangle par son milieu en passant par une zone favorable au développement des glaçures au fer de type «gouttes d’huile». Nous accéderons aux diagrammes 21-36-48-56 en passant à égale distance des diagrammes 13-14, 28-29, 42-43, 52-53, et 58-59.
J’en profite pour ouvrir une petite parenthèse et signaler qu’il n’est pas interdit de rechercher à mi-chemin de deux des diagrammes existants et qu’on peut formuler une glaçure à partir d’une mole basique intermédiaire. Avec une mole basique établie à 0,25 CaO, 0,25 MgO et 0,5 KnaO nous nous situons à égale distance des diagrammes 42 et 43.
Le talc nous apporte MgO et associé à un feldspath va nous permettre de parcourir l’arête des diagrammes 32-39-45-50-54-57 et 59. On accédera ainsi entre autres à une zone favorable aux «blancs magnésiens».
Feldspath, chaux, dolomie et talc vont donc nous permettre d’aborder simplement et rapidement un grand nombre de diagrammes de fusion.
Il ne manque plus que deux autres matières premières pour pouvoir se déplacer à volonté à l’intérieur de ces diagrammes de fusion : il s’agit du quartz et du kaolin.
Un diagramme de fusion offre un vaste choix d’essais possibles. Alors, par où va-t-on démarrer, quel premier essai va-t-on choisir ? En réalité c’est le feldspath qui présent dans une grande majorité des cas peut décider de ce premier choix.
Prenons par exemple le diagramme n°33 dont la mole basique est 0,4 KNaO 0,6 CaO. Je vais y accéder en associant chaux : CaCO3, masse molaire 100 et le feldspath potassique dont nous avons calculé la formule : KNaO 1,14 Al2O3 7,32 SiO2, masse molaire 643.
Je prendrai donc 0,4 feldspath pour fournir les 0,4 KNaO demandés par la mole basique du diagramme n°33. En plus d’apporter 0,4 KNaO, le feldspath apportera aussi 0,4 × 1,14 = 0,45 Al2O3 ainsi que 0,4 × 7,32 = 2,93 SiO2 (résultats arrondis à deux chiffres après la virgule).
Nous avons deux valeurs qui vont définir un point A sur le diagramme de fusion, point de départ de notre recherche qui correspond déjà à une recette théoriquement exploitable puisque située au cœur de la zone définie par Daniel de Montmollin. C’est une recette simple ne comportant que deux matières premières et que nous allons calculer.
KNaO 0,4 CaO 0,6 Al2O3 SiO2 Feldspath 0,4 0,4 0,45 2,93 Chaux 0,6 0,6 Point A 0,4 0,6 0,45 2,93
Tableau 1.3: Le point A dans le diagramme n°33.
Ce point correspond à la recette suivante :
| Feldspath | 0,4 × 643 | = | 257,2 | : | 317,2 × 100 = 81,1 |
| Carbonate de chaux | 0,6 × 100 | = | 60,0 | : | 317,2 × 100 = 18,9 |
| 317,2 |
A partir de ce point, il sera possible de se déplacer dans le diagramme n°33 tout en visualisant clairement les apports des nouveaux éléments que sont le quartz et le kaolin.
Un trait tiré à la verticale du point A permet de visualiser la progression des apports possibles de quartz.
On voit tout de suite que l’on va pouvoir accéder à la zone définie par Daniel de Montmollin comme étant favorable à l’obtention des glaçures de type «bleu de fer».
Je décide donc de réaliser un deuxième essai désigné par le point B à 4 moles de silice au-dessus du point A.
Je reprends le tableau précédemment établi pour calculer le point A et je le complète en y incorporant la quantité molaire de silice nécessaire pour accéder au point B.
KNaO 0,4 CaO 0,6 Al2O3 SiO2 Feldspath 0,4 0,4 0,45 2,93 Chaux 0,6 0,6 Quartz 4 4,00 Point B 0,4 0,6 0,45 6,93
Tableau 1.4: L’apport de quartz dans le diagramme n°33.
A cette nouvelle formule, correspond la recette :
| Feldspath | 0,4 × 643 | = | 257,2 | : | 557,2 × 100 = 46,2 |
| Carbonate de chaux | 0,6 × 100 | = | 60,0 | : | 557,2 × 100 = 10,8 |
| Quartz | 4,0 × 60 | = | 240,0 | : | 557,2 × 100 = 43,0 |
| 557,2 |
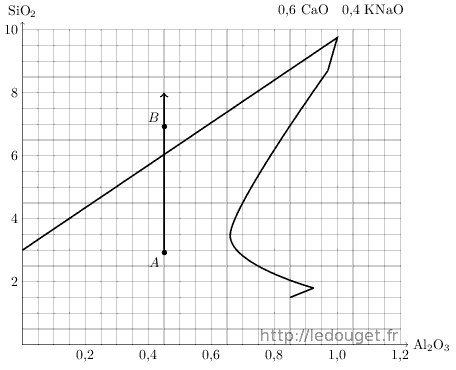
Figure 1.3: Diagramme n°33, l’apport de quartz.
Toujours à partir du point A, nous allons maintenant nous déplacer vers la droite du diagramme. On pourra visualiser les apports de kaolin comme on l’a fait plus haut pour le quartz. Notre progression ne se fera pas à l’horizontale mais en oblique car il ne faut pas oublier que le kaolin n’apporte pas seulement de l’alumine mais aussi de la silice dans le rapport d’une mole d’alumine pour deux moles de silice.
Par commodité, on repérera un point distant de 0,5 mole d’Al2O3 à droite et à la même hauteur que le point A, puis on y ajoutera verticalement une mole de silice pour fixer un second point. La droite partant de A et passant par ce point permettra de visualiser tous les apports possibles de kaolin.
Nous allons réaliser un troisième essai au point C qui se situe dans une zone définie comme favorable aux «temmoku» ou noirs de fer.
Pour passer du point A au point C choisi, je dois faire l’apport de 0,3 mole d’alumine. Je reprends encore une fois le tableau établi pour définir et calculer le point A et j’y intègre le nouvel apport, celui du kaolin.
KNaO 0,4 CaO 0,6 Al2O3 SiO2 Feldspath 0,4 0,4 0,45 2,93 Chaux 0,6 0,6 Kaolin 0,3 0,30 0,60 Point C 0,4 0,6 0,75 3,53 .
Tableau 1.5: L’apport du kaolin dans le diagramme n°33.
A cette nouvelle formule correspond la recette :
| Feldspath | 0,4 × 643 | = | 257,2 | : | 394,6 × 100 = 65,2 |
| Carbonate de chaux | 0,6 × 100 | = | 60,0 | : | 394,6 × 100 = 15,2 |
| Kaolin | 0,3 × 258 | = | 77,4 | : | 394,6 × 100 = 19,6 |
| 394,6 |
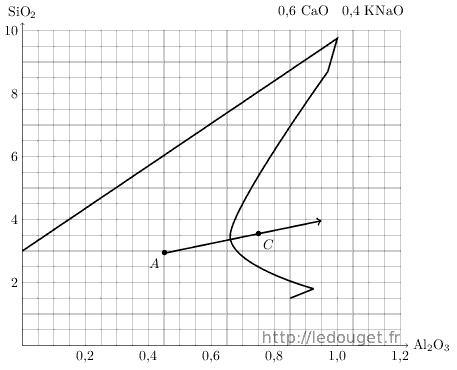
Figure 1.4: Diagramme n°33, l’apport de kaolin.
A partir d’un point A sur un diagramme de fusion correspondant à l’apport de deux premiers composants, nous avons défini le long de deux axes toute une série de recettes possibles par l’apport d’un troisième élément, soit dans un cas le quartz, soit dans l’autre le kaolin.
Ces deux axes délimitent une zone qui elle, ne sera accessible que par les apports combinés du quartz et du kaolin. De chaque point de l’axe figurant les apports de quartz, il sera possible de se déplacer sur la droite par des apports de kaolin. De la même façon on pourra tout aussi bien se déplacer à la verticale par des apports de quartz à partir de chaque point de l’axe figurant les apports de kaolin.
On voit donc clairement que toute une partie du diagramme de fusion n’est pas accessible simplement du fait que sodium et potassium sous forme insoluble sont généralement fournis aux glaçures par les feldspaths qui apportent en même temps et forcément une part importante d’alumine et de silice. Pour accéder à la «zone fritte» indiquée par Daniel de Montmollin, il faut alors apporter différemment le sodium et le potassium rendus insolubles par fusion, associés à d’autres éléments dans ces matériaux nommés «frittes» qui sont fournies par l’industrie.
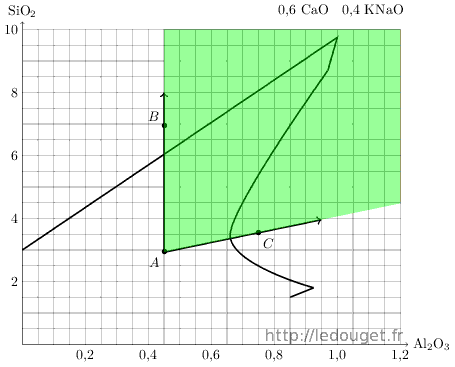
Figure 1.5: Diagramme n°33, zone explorable.
Il est tout de même possible d’élargir quelque peu cette zone de recherche sans faire appel à une «fritte» du commerce, simplement en disposant également d’un «feldspathoïde» un peu particulier qui l’on nomme syénite néphéline.
Ce feldspath a en effet la particularité d’être bien plus pauvre en silice que la plupart des autres feldspaths. La formule recalculée d’une syénite fournie par Céradel Socor m’a donné la formule suivante : KNaO Al2O3 4,2 SiO2 avec une masse molaire de 446.
Dans ce même diagramme n°33, la syénite me fournirait pour ma recherche un point de départ A’ bien plus bas que A. Voici sur le diagramme 1.6 les deux zones comparées.
KNaO 0,4 CaO 0,6 Al2O3 SiO2 Syénite 0,4 0,4 0,4 1,68 Chaux 0,6 0,6 Point A’ 0,4 0,6 0,4 1,68
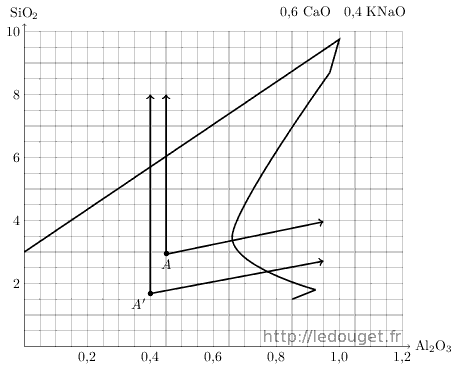
Figure 1.6: Points A et A′ sur le diagramme n°33.
Pour se familiariser avec le calcul, je propose d’accéder à deux nouveaux diagrammes comme nous l’avons déjà fait pour le diagramme n°33 avec le carbonate de chaux associé au feldspath. Cette fois nous associerons d’abord dolomie et feldspath pour accéder au diagramme n°48, dans la zone des émaux à «gouttes d’huile» puis nous associerons le talc au feldspath pour atteindre le diagramme n°39 favorable lui aux «blancs magnésiens».
Nous ferons un premier calcul avec le feldspath potassique puis nous remplacerons celui-ci par la syénite pour visualiser un second point d’accès possible dans ces mêmes diagrammes.
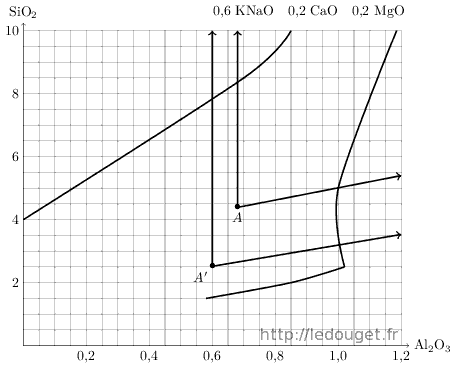
Figure 1.7: Points A et A′ sur le diagramme n°48.
Pour accéder au diagramme n°48, nous allons donc utiliser le feldspath potassique de formule : KNaO 1,14 Al2O3 7,32 SiO2 masse molaire : 643. Nous l’associons à la dolomie dont nous gardons la formule théorique : CaCO3 MgCO3 masse molaire : 184. La mole basique du diagramme n°48 est : 0,6 KNaO 0,2 CaO 0,2 MgO.
Nous allons définir notre point d’accès au diagramme dans le tableau 1.6.
KNaO 0,6 CaO 0,2 MgO 0,2 Al2O3 SiO2 Feldspath 0,6 0,6 0,68 4,39 Dolomie 0,2 0,2 0,2 Point A 0,6 0,2 0,2 0,68 4,39
Tableau 1.6: Le point A dans le diagramme n°48.
Le point A correspond à la recette suivante :
| Feldspath potassique | 0,6 × 643 | = | 385,8 | : | 422,6 × 100 = 91,3 |
| Dolomie | 0,2 × 184 | = | 36,8 | : | 422,6 × 100 = 8,7 |
| 422,6 |
Si nous choisissons de prendre de la syénite néphéline dont je rappelle la formule : KNaO Al2O3 4,2 SiO2 masse molaire : 446, nous accéderons dans le même diagramme au point A’ à 0,6 Al2O3 2,52 SiO2.
Enfin comme dernier exemple, prenons le diagramme n°39 (cf. figure 1.8) sur l’arête accessible en associant feldspath et talc. Sa mole basique est : 0,4 KNaO 0,6 MgO
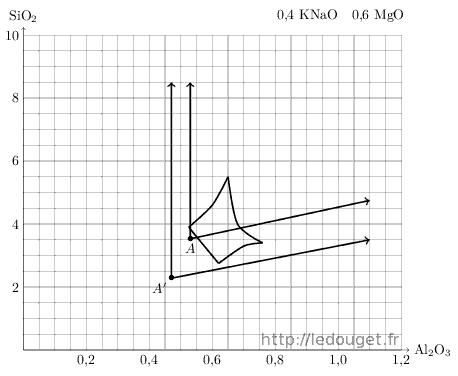
Figure 1.8: Points A et A′ sur le diagramme n°39.
Le talc choisi a la formule suivante : MgO 0,12 Al2O3 SiO2 masse molaire 126. Associé au feldspath potassique, il nous donne le tableau 1.7.
KNaO 0,6 MgO 0,2 Al2O3 SiO2 Feldspath 0,4 0,4 0,46 2,93 Talc 0,6 0,6 0,07 0,60 Point A 0,4 0,6 0,53 3,53
Tableau 1.7: Le point A sur le diagramme n°39.
Ce point A correspond à la recette suivante :
| Feldspath potassique | 0,4 × 643 | = | 257,2 | : | 332,8 × 100 = 77,3 |
| Talc | 0,6 × 126 | = | 75,6 | : | 332,8 × 100 = 22,7 |
| 332,8 |
En remplaçant le feldspath potassique par de la syénite nous accédons au point A’ à 0,47 Al2O3 2,28 SiO2 qui correspond à la recette suivante :
| Syénite | 0,4 × 446 | = | 178,4 | : | 254 × 100 = 70 |
| Talc | 0,6 × 126 | = | 75,6 | : | 254 × 100 = 30 |
| 254,0 |
Après avoir sélectionné un certain nombre de diagrammes par le choix des matières premières et après avoir défini dans ces diagrammes les zones les plus facilement et rapidement accessibles, il nous faut désormais passer à la réalisation pratique des essais.
Mais là encore, il sera possible de simplifier la procédure et de limiter singulièrement le nombre des calculs et des pesées.
Reprenons l’exemple du diagramme n°33. Nous avons accédé au point A de ce diagramme à 0,45 Al2O3 2,93 SiO2 qui correspond à la recette :
| Feldspath potassique | : | 81,1 |
| Carbonate de chaux | : | 18,9 |
Par un apport de kaolin, nous nous sommes déplacés jusqu’au point C à 0,75 Al2O3 3,53 SiO2 qui correspond à la recette :
| Feldspath potassique | : | 65,2 |
| Carbonate de chaux | : | 15,2 |
| Kaolin | : | 19,6 |
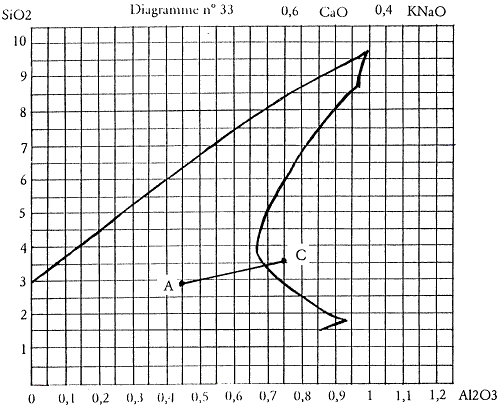
Figure 2.1: Diagramme n°33, mélange en ligne AC.
Entre les points A et C, il existe évidemment de nombreuses possibilités intermédiaires qu’il serait fastidieux de devoir toutes calculer et encore plus réaliser. La multiplication des calculs et la multiplication des pesées demanderaient un temps infini. Il y a mieux à faire et pour cela nous allons choisir un procédé simple et rapide que l’on appelle «mélange en ligne». Voici la procédure :
| Essai n° | 1 | 2 | 3 | 4 | 5 | 6 |
| Recette A | 5 g | 4 g | 3 g | 2 g | 1 g | 0 g |
| Recette C | 0 g | 1 g | 2 g | 3 g | 4 g | 5 g |
Je réalise ainsi une série de 6 essais de 5 g chacun. Les essais intermédiaires n’auront pas nécessité de calcul pour établir leur formule ni calculer leur recette. Le nombre de pesées pour réaliser ces essais intermédiaires aura également été réduit même si pour une glaçure aussi simple le gain de temps n’est pas très significatif. Mais imaginez maintenant une glaçure à 8 ou 10 composants et vous saisirez tout l’intérêt du mélange en ligne.
J’ajoute maintenant dans chaque gobelet la quantité d’eau nécessaire pour délayer la glaçure et en assurer l’homogénéité à l’aide d’un pinceau. Je verse le contenu du gobelet à l’arrière d’une plaquette à essai en forme de L en répartissant l’émail en une couche épaisse et régulière à l’aide du même pinceau.
Chaque plaquette doit évidemment recevoir sur l’autre côté inscrit à l’oxyde de fer toutes les indications nécessaires : diagramme, référence de l’émail et n°d’ordre de la plaquette.
Au moment de la cuisson, il sera important que la série de plaquettes reste bien groupée pour que des différences de température ou d’atmosphère de cuisson ne viennent pas fausser l’interprétation des résultats.
En plus de trouver des recettes exploitables, cette méthode de mélange en ligne permet aussi de comprendre le comportement d’un élément donné puisque dans le cas présent il est le seul à varier de façon progressive dans l’émail. Dans l’exemple choisi, on comprendra le rôle du kaolin et plus précisément la fonction de l’alumine dans la fusion et l’aspect des essais.
Restons toujours dans l’exemple choisi du diagramme n°33 et de cette progression de kaolin du point A vers le point C. Imaginons qu’après cuisson des 6 essais réalisés, le n°3 se révèle le meilleur. Il est composé de 3 parts de la recette A pour 2 parts de la recette C.
Sa recette en pourcentage ne sera pas difficile à calculer :
| Recette A | Feldspath potassique | 81,1 × 3 : 5 | = | 48,7 |
| Carbonate de chaux | 18,9 × 3 : 5 | = | 11,3 | |
| Recette C | Feldspath potassique | 65,2 × 2 : 5 | = | 26,1 |
| Carbonate de chaux | 15,2 × 2 : 5 | = | 6,1 | |
| Kaolin | 19,6 × 2 : 5 | = | 7,8 | |
| Recette | Feldspath potassique | 48,7 + 26,1 | = | 74,8 |
| Essai n°3 | Carbonate de chaux | 11,3 + 6,1 | = | 17,4 |
| Kaolin | 7,8 |
Je peux évidemment me contenter de la recette pondérale de cet essai n°3. Cependant si je désire connaître la formule unité correspondant à cette recette et pouvoir ainsi la positionner sur le diagramme de fusion, je procède de la façon suivante :
Je divise les quantités de matières premières par les masses molaires correspondantes.
| Feldspath potassique | 74,8 | : | 643 | = | 0,1163 |
| Carbonate de chaux | 17,4 | : | 100 | = | 0,1740 |
| Kaolin | 7,8 | : | 258 | = | 0,0302 |
Je vais multiplier ensuite la quantité molaire de chaque matériau par la quantité de chacun des oxydes indiqué dans sa formule. Cela va me donner :
Une fois ces calculs faits, nous pouvons les disposer dans le tableau 2.1 pour obtenir dans la dernière rangée la formule provisoire.
KNaO CaO Al2O3 SiO2 Feldspath 0,1163 0,1163 0,1326 0,8513 Chaux 0,174 0,1740 Kaolin 0,0302 0,0302 0,0604 Formule provisoire 0,1163 0,1740 0,1628 0,9117
Tableau 2.1: Formule provisoire.
Pour obtenir la formule unité définitive, je ramène le total de la mole basique à 1 puis je divise Al2O3 et SiO2 par ce même diviseur, ce qui me donne :
| KNaO | 0,1163 | : | 0,2903 = 0,4 | Al2O3 | 0,1628 : 0,2903 = 0,56 | |
| CaO | 0,174 | : | 0,2903 = 0,6 | SiO2 | 0,9117 : 0,2903 = 3,14 | |
| 0,2903 |
La formule unité de cet essai n°3 est donc : 0,4 KNaO 0,6 CaO 0,56 Al2O3 3,14 SiO2 et nous pouvons le positionner sur le diagramme de fusion (cf. figure 2.2).
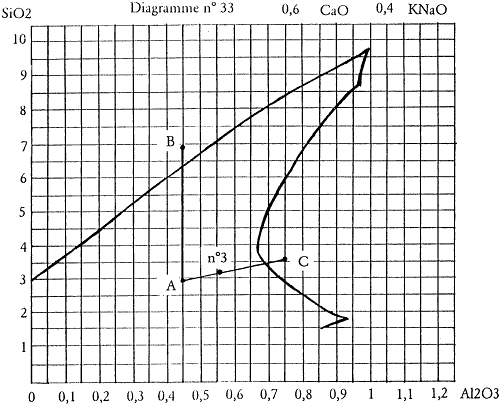
Figure 2.2: Position de l’essai n°3 sur le diagramme.
Si dans le cas présent, ce calcul vous paraît un peu long, fastidieux et en un mot peu justifié, sachez qu’il est important de maîtriser cette démarche car c’est celle qu’il faudra adopter chaque fois que vous voudrez obtenir la formule d’un émail à partir d’une simple recette. Il vous suffira pour cela de connaître les formules des matières premières qui la composent. Vous pourrez ainsi, même si vous n’utilisez pas de matières semblables, recalculer à partir de cette formule une nouvelle recette avec vos propres matériaux. Avec un peu de pratique vous verrez aussi que la seule façon efficace de comprendre un émail et de le comparer à un autre est de le faire à partir de la formule unité.
Pour revenir au mélange en ligne et en observant le diagramme de fusion n°33, nous voyons qu’il serait possible de la même façon d’étudier la progression de la silice entre les points A et B. Toutefois, si nous voulons aborder et étudier une zone plus vaste délimitée sur le diagramme par les deux droites AC et BC, on fera le choix d’un autre type de mélange : le mélange ternaire.
Nous avons déjà rencontré au début de cet exposé un exemple de mélange ternaire avec le triangle représentant les 60 diagrammes de Daniel de Montmollin.
En réalité, ce triangle aurait du comporter 66 points représentant les 66 rapports différents possibles entre les trois composants, la progression se faisant de la base vers le sommet, de 0,1 mole en 0,1 mole de 0 jusqu’à 1.
Dans un souci toujours constant de limiter le temps consacré à l’élaboration des essais sans pour autant nuire à l’interprétation des résultats, j’ai fait le choix d’une progression de 1 g en 1 g de 0 jusqu’à 5 g (puisqu’il s’agit ici de pesées) pour obtenir un mélange ternaire de 21 essais.
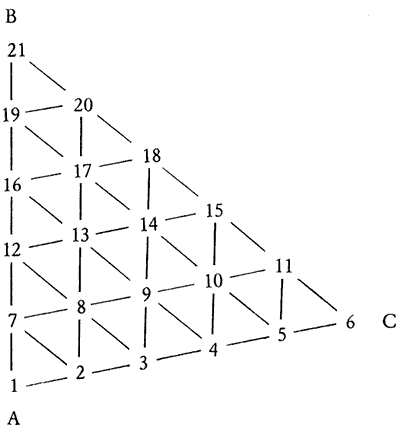
Figure 2.3: Représentation du mélange ternaire et numérotation des 21 essais.
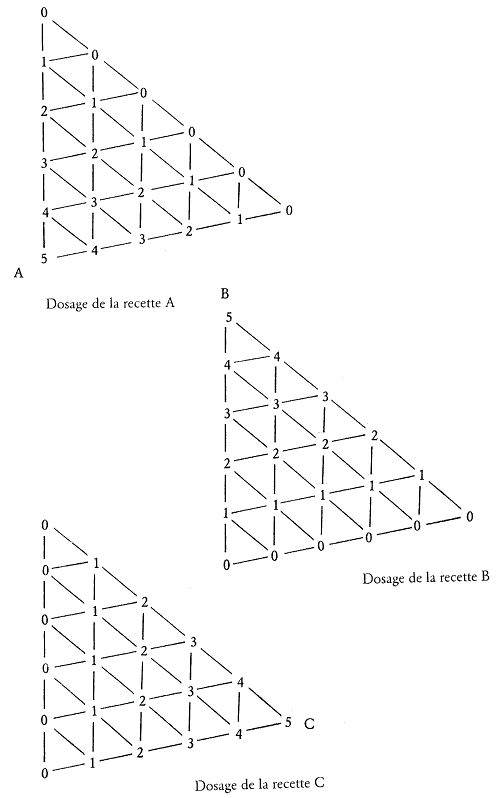
Figure 2.4: Mélange ternaire à 21 essais.
La figure 2.3 représente ce mélange ternaire, tel qu’il pourra figurer dans un diagramme de fusion entre les deux axes représentant les progressions de kaolin et de silice.
Si je reprends l’exemple du diagramme n°33, il suffira de relier les points B et C pour définir la zone de recherche de mon mélange ternaire. Les points A, B et C deviennent les sommets du triangle.
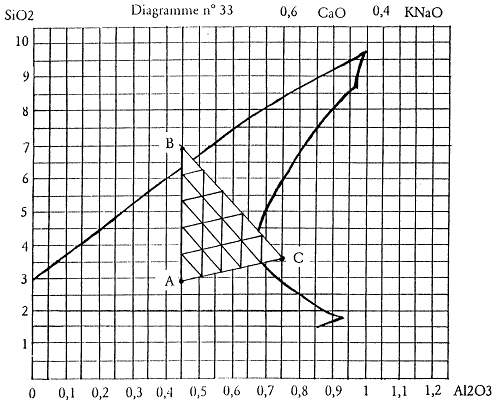
Figure 2.5: Le triangle ABC dans le diagramme n°33.
Je définis et calcule d’abord les trois recettes qui composent les trois sommets du triangle. Dans l’exemple choisi, nous avons déjà calculé ces trois recettes qui sont :
| Recette A | Recette B | ||
| Feldspath potassique | 81,1 | Feldspath potassique | 46,2 |
| Carbonate de chaux | 18,9 | Carbonate de chaux | 10,8 |
| Quartz | 43,0 | ||
| Recette C | |||
| Feldspath potassique | 65,2 | ||
| Carbonate de chaux | 15,2 | ||
| Kaolin | 19,6 |
Je prépare ensuite 35 g de chacune de ces trois recettes. Nous avons vu précédemment l’emploi de la règle de trois pour recalculer chaque recette en conséquence : ici chaque quantité est multipliée par 35 puis divisée par 100.
En effet il faut avoir le souci constant d’économiser les matières premières et de ne préparer que la stricte quantité nécessaire : 5 g pour chaque essai suffit largement à l’émaillage d’une plaquette.
Je réalise l’homogénéité de chacune de ces trois recettes par deux ou trois passages à sec au tamis.
Je dispose mes 21 gobelets en plastique dans l’ordre des essais comme indiqué sur la figure 2.3.
J’effectue les pesées comme indiquées sur les trois schémas page ?? en ayant bien soin de toujours démarrer de la base vers le sommet. En effet, si par accumulation de légères erreurs de pesées, il ne restait pas exactement 5 g pour le dernier essai, c’est-à-dire le sommet, cela n’aurait aucune incidence sur la composition de celui-ci.
Au final, je me retrouve donc avec 21 essais de 5 g chacun. J’émaille mes plaquettes à essai comme indiqué précédemment pour le mélange en ligne. Je marquerai lisiblement tout repère nécessaire au dos des plaquettes et je ferai en sorte de les garder groupées sur la plaque d’enfournement au moment de la cuisson. Comme déjà dit, des différences de température ou d’atmosphère de cuisson sur des plaquettes dispersées dans le four pourraient totalement fausser l’interprétation des résultats.
Imaginons que l’essai n°10 se révèle particulièrement intéressant. Calculons sa recette, elle correspond à l’addition de : 1/5 de la recette A, 1/5 de la recette B et 3/5 de la recette C.
Plus précisément l’essai n°10 a la composition suivante :
| Feldspath potassique | (81,1 × 1:5)+(46,2 × 1 : 5)+(65,2 × 3:5) = | 64,6 |
| Carbonate de chaux | (18,9 × 1:5)+(10,8 × 1 : 5)+(15,2 × 3:5) = | 15,0 |
| Quartz | (43,0 × 1:5) = | 8,6 |
| Kaolin | (19,6 × 3:5)= | 11,8 |
| 100,0 |
Si je désire calculer sa formule unité et le positionner sur le diagramme de fusion, je divise les quantités de chacun des composants par sa masse molaire correspondante :
| Feldspath potassique | 64,6 : 643 | = | 0,1005 |
| Carbonate de chaux | 15,0 : 100 | = | 0,1500 |
| Quartz | 8,6 : 60 | = | 0,1433 |
| Kaolin | 11,8 : 258 | = | 0,0457 |
Je réalise le tableau 2.2 pour établir la formule provisoire de cet essai n°10. Je ramène la mole basique à 1.
KNaO CaO Al2O3 SiO2 Feldspath 0,1005 0,1005 0,1146 0,7357 Chaux 0,15 0,15 Quartz 0,1433 0,1433 Kaolin 0,0457 0,0457 0,0914 Formule provisoire 0,1005 0,15 0,1603 0,9704
Tableau 2.2: Diagramme n°33, formule provisoire de l’essai n°10.
| KNaO | 0,1005 | : | 0,2505 | = | 0,4 |
| CaO | 0,1500 | : | 0,2505 | = | 0,6 |
| 0,2505 | 1,0 |
Et je divise les quantités d’alumine et de silice par le même commun diviseur (0,2505) pour obtenir la formule unité définitive : 0,4 KNaO 0,6 CaO 0,64 Al2O3 3,88 SiO2
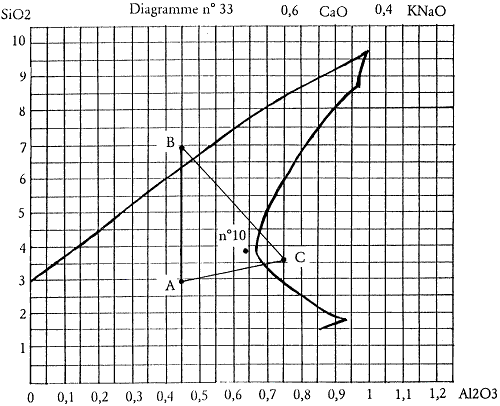
Figure 2.6: Position de l’essai n° 10 sur le diagramme.
Au vu des résultats, je considère qu’aucun essai ne répond à mon attente mais je pense discerner dans une zone délimitée par trois essais une possibilité intéressante. Il sera alors possible d’affiner la recherche et par un effet de «zoom avant» d’établir un nouveau mélange ternaire dont les nouveaux sommets seront les trois essais retenus.
Le mélange ternaire que nous avons établi dans le diagramme n°33 ne couvre pas toute la zone théoriquement exploitable définie par le tracé proposé par Daniel de Montmollin.
Il apparaît évident qu’il serait intéressant de définir un quatrième point à la verticale du point C et ainsi d’augmenter le champ de recherche par tous les mélanges possibles entre les quatre recettes formant les quatre sommets de ce quadrilatère.
Avant d’étudier les possibilités qui nous sont offertes pour ce type de mélange, nous pouvons déjà établir la formule et la recette de ce quatrième point que nous nommerons D.
Nous allons partir des calculs et du tableau réalisés pour la définition et la recette du point C et décider d’un apport de quartz qu’il reste à définir. Au vu du tracé établi par Daniel de Montmollin, je propose d’augmenter le point C de 4 moles de silice, ce qui était déjà la valeur que nous avions retenue pour définir le point B à partir du point A. Le tableau 2.3 nous donne la formule unité du point D.
KNaO 0,4 CaO 0,6 Al2O3 SiO2 Feldspath 0,4 0,4 0,45 2,93 Chaux 0,6 0,6 Koalin 0,3 0,30 0,60 Quartz 4 4,00 Point D 0,4 0,6 0,75 7,53
Tableau 2.3: Formule unité du point D du diagramme n°33.
A cette nouvelle formule correspond la recette :
| Feldspath | 0,4 × 643 | = | 257,2 | : | 634,6 × 100 = 40,5 |
| Carbonate de chaux | 0,6 × 100 | = | 60,0 | : | 634,6 × 100 = 9,5 |
| Kaolin | 0,3 × 258 | = | 77,4 | : | 634,6 × 100 = 12,2 |
| Quartz | 4,0 × 60 | = | 240,0 | : | 634,6 × 100 = 37,8 |
| 634,6 |
Dans ce mélange de type quaternaire, il faudra trouver une méthode qui nous permette d’obtenir des essais intermédiaires équitablement répartis dans la zone étudiée et qui nécessitent un minimum de pesées.
Dans son livre «Stoneware glazes: a systematic approach» l’Australien Ian Currie propose de relier les sommets entre eux par des mélanges en ligne, puis de la même façon tous les mélanges intermédiaires. Dans l’exemple d’un mélange quaternaire à 36 essais (six essais par côté) cela nécessiterait exactement 100 pesées.
Cette proposition qui paraît évidente n’est pourtant pas celle que je retiens et cela pour deux raisons. En effet, il y a une possibilité de réaliser ces 36 essais en effectuant seulement 80 pesées au lieu des 100 de la méthode précédente. De plus, la méthode que je propose permet de passer sans aucune modification du dosage par pesées au dosage en volume (et plus précisément «en gouttes») que je compte aborder et développer plus loin dans cet exposé. En effet, nous conserverons toujours dans les mélanges intermédiaires des dosages en nombres entiers et cela, que nous progressions de 0 à 10 g ou de 0 à 10 gouttes. Ce dosage en gouttes n’est pas possible dans les mélanges intermédiaires avec un chiffre après la virgule dans la méthode Currie. On peut travailler au dixième de gramme mais pas au dixième de goutte évidemment !
En réalité, je propose de ne pas quitter véritablement le mélange ternaire mais plutôt d’en réaliser deux et de les associer pour aboutir à un mélange quaternaire. Les sommets B et C étant communs aux deux triangles, il existe donc une médiane commune BC qui comportera six essais qui ne seront bien évidemment réalisés qu’une seule fois.
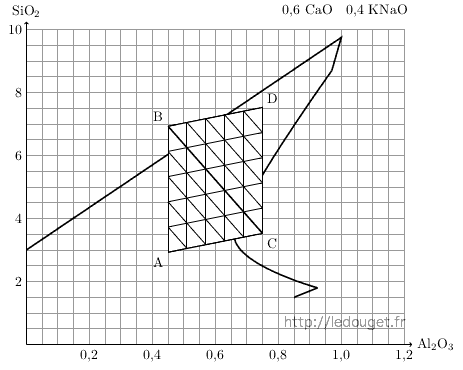
Figure 2.7: Diagramme n°33, le mélange quaternaire ABCD.
En additionnant donc deux mélanges ternaires à 21 essais nous arrivons à un mélange quaternaire à 36 essais tout comme pour la méthode Currie. Le gain réalisé au nombre des pesées à effectuer provient du fait que la recette du sommet A n’interviendra pas dans le triangle BDC tout comme le sommet D ne le fera pas pour le triangle ABC.
Il faudra être très vigilant au moment d’effectuer les pesées et faire bien attention à visualiser les bases et les sommets opposés. Les sommets A et D ont une base commune qui est la médiane BC mais les sommets B et C possèdent chacun deux bases opposées. Les schémas de la page ?? montreront de façon plus claire la répartition des pesées.
Pour 36 essais de 5 g chacun, il faut préparer 35 g des recettes A et D, mais 55 g des recettes B et C qui interviennent dans les deux mélanges ternaires associés. Si vous avez la possibilité de doubler les cuissons (oxydation et réduction), doublez les plaquettes en préparant double quantité, soit 70 g de A et D et 110 g de B et C.
La progression des pesées ne sera plus alors : 1-2-3-4-5 g mais 2-4-6-8-10 g.
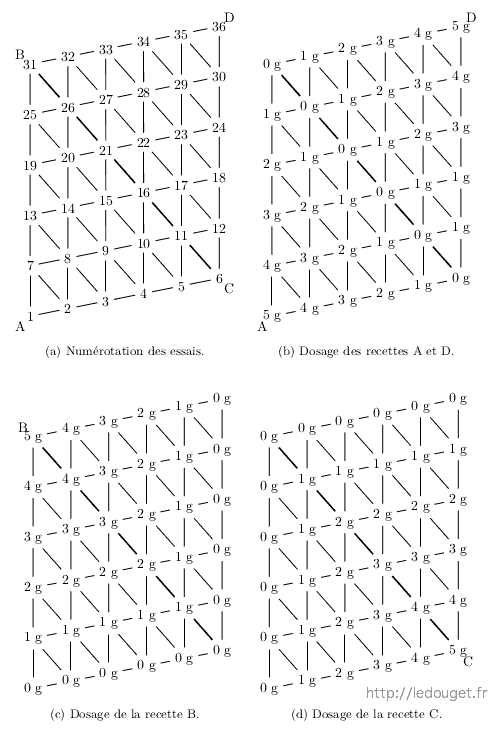
Figure 2.8: Mélange quaternaire à 36 essais.
Je profite de l’occasion qui m’est donnée par la rédaction de cet exposé pour rendre hommage à Jean Messein qui fut l’inventeur de cette méthode de dosage qu’il exposa dans les colonnes de la «céramique moderne» il y a déjà 30 ans.
Même si je me suis permis de l’adapter et de la transformer à ma propre convenance, je dois reconnaître après de nombreuses années de pratique que cette méthode a prouvé toute sa fiabilité. Ce qui est étonnant, c’est que dans la littérature céramique anglo-saxonne, il est souvent proposé des méthodes de dosage en volume avec mise en suspension des glaçures et prises d’échantillons à l’aide d’une seringue. Mais, que ce soit Ian Currie ou Greg Dally, aucun n’a eu l’idée de franchir le pas qui mène du millilitre à la goutte.
Le dosage en gouttes est un procédé qui permet un gain de temps important comparé à la méthode classique par pesées car ici, seuls les sommets du mélange sont pesés, tous les essais intermédiaires étant ensuite dosés en gouttes directement sur la plaque à essais.
C’est également un procédé extrêmement économe en matières premières puisqu’au final chacun des essais n’utilise pas plus de 0,25 g de matière sèche. On peut y adapter tous les procédés que nous avons déjà étudiés depuis le début de cet exposé : mélange en ligne, mélange ternaire et mélange quaternaire.
L’interprétation des résultats demande sans doute une certaine habitude et n’offre pas la possibilité de juger vraiment de la fusibilité d’un émail et plus précisément de son écoulement sur une paroi verticale comme on le fait sur une plaquette classique en forme de L.
Cependant, l’aspect de surface, le développement de la couleur et même la tension superficielle sont parfaitement observables. C’est une méthode d’approche qui permet de trouver rapidement les zones exploitables, de cibler la recherche avant de passer à la réalisation d’essais de grande taille ou de petites pièces témoins.
Avant d’expliquer plus en détail le procédé et sa mise en application, je voudrais décrire le support nécessaire à cette méthode.
Il s’agit de réaliser des plaquettes en argile comportant un certain nombre d’alvéoles que l’on passera au four de dégourdi avant utilisation. Voici le modèle que j’utilise en priorité pour réaliser les mélanges à quatre recettes, en réalité l’association de deux mélanges ternaires comme nous l’avons déjà vu.
Pour réaliser ces plaquettes, j’ai d’abord découpé un gabarit en contre-plaqué pour obtenir un carré de 12 cm de côté. Sur ce carré, je trace au crayon un autre carré qui lui fera 7,5 cm de côté et sur lequel je vais positionner les 36 points représentant les 36 essais. Ces points seront distants de 1,5 cm. Je fixe alors sur ces 36 points des clous de tapissier à tête ronde de 1 cm de diamètre.
C’est ce gabarit qui va me permettre de marquer des empreintes dans ma plaque d’argile étalée au rouleau et épaisse de 1 à 1,2 cm. Ne pas oublier d’intercaler une feuille plastifiée entre gabarit et argile. Je découpe alors mes plaques à la taille extérieure du gabarit. La marge entre le bord extérieur et la zone des alvéoles servira en temps voulu à inscrire sur la plaquette tout renseignement nécessaire sur la nature des essais, l’atmosphère de cuisson, etc.
Je laisse durcir mes plaquettes d’argile, intercalées entre des petites plaques de placoplâtre pour éviter tout gauchissement. Quand les plaquettes ont atteint la «consistance du cuir» je creuse les 36 cavités à l’aide d’une mèche à béton de 11 mm de diamètre sur une profondeur de 5 à 7 mm estimée au jugé. L’idéal est d’utiliser pour cela une visseuse ou une petite perceuse sans fil.
Le principe du dosage ne change pas par rapport au principe des différents mélanges que nous avons étudiés précédemment. Quand nous faisions des progressions de gramme en gramme par pesées successives , nous ferons désormais des dosages de goutte en goutte, le compte-gouttes ayant remplacé la balance. A ce sujet je conseille d’utiliser les petits flacons en verre surmontés d’un embout en plastique souple que l’on presse. C’est un modèle que l’on trouve en pharmacie comme contenant de collyre telle la Bacitracine.
Après avoir fait les pesées pour préparer les sommets du mélange, je conseille de les passer au moins une fois au travers d’un tamis pour obtenir une dispersion parfaite et éviter tout grumeau après apport de l’eau dans l’émail.
Il faudra que l’émail soit fluide pour bien s’écouler du doseur, bien plus que pour l’émaillage d’une plaquette. Il s’agit de peser précisément l’eau et d’en mettre le double en poids par rapport à la matière sèche. C’est-à-dire que si vous préparez 5 g de matière sèche pour chacun des 4 sommets de votre mélange quaternaire, vous ajouterez 10 g d’eau à chacune de ces recettes.
Avant de commencer le dosage, on indique au crayon gris sur les marges de la plaquette les repères et indications nécessaires.
Une fois le compte-gouttes rempli et la répartition des gouttes commencée, on n’oublie pas de secouer régulièrement le compte-gouttes pour maintenir les matières en suspension et conserver un émail bien homogène.
Les dosages se feront de 2 gouttes en 2 gouttes pour une plaquette à 36 essais, de 0 à 10 en partant de la base de chaque triangle vers son sommet comme nous l’avons déjà expliqué. Pour les pesées, nous avions estimé qu’un total de 5 g était suffisant pour une plaquette à essai. Ici, il nous faut 10 gouttes par alvéole pour disposer d’une quantité d’émail nécessaire et suffisante pour juger du résultat.
Il suffit de se reporter aux schémas déjà établis pour les pesées dans le mélange quaternaire, à une différence prêt, c’est que nous progresserons ici de 2 en 2 gouttes de 0 à 10 alors que nous progressions de 1 g en 1 g de 0 à 5. Mais le principe reste le même.
Une fois le dosage terminé, il nous reste encore à homogénéiser les essais intermédiaires car les dosages successifs sont superposés et non mélangés. On sature alors d’eau chacune des alvéoles à l’aide d’une poire à engobe et on remue chaque essai à l’aide d’un petit bâtonnet. On laissera sécher les plaquettes et on pourra alors remplacer les indications au crayon gris par des inscriptions à l’oxyde de fer.
Pour finir, je voudrais juste signaler que si l’utilisation de toutes les matières est possible dans cette méthode, il vaut mieux cependant utiliser Kaolin et argiles sous leur forme calcinée. Une matière crue demande une plus grande quantité d’eau pour une fluidité suffisante et nous risquerions dans le cas présent d’avoir un émail trop épais pour un bon dosage en gouttes.
Cependant, quand il s’agira de préparer un émail en quantité importante, il est toujours avantageux d’y intégrer au moins 10 % de matière crue. Cela permet en effet une meilleure adhérence de l’émail au tesson, une plus grande dureté de la couche d’émail facilitant la manipulation des pièces et enfin une meilleure suspension du bain avec moins de risque de «plombage».
On pourra facilement modifier sa recette en conséquence à condition d’avoir calculé la perte au feu de son argile ou de son kaolin. On dégourdit 100 g de la matière et on pèse au défournement. Si par exemple il reste 88 g, ma perte au feu est donc de 12 g. Pour 100 g de matière calcinée, je mettrai donc dans mon émail : (12 × 100 / 88) + 100 = 113,6 g de matière crue.
Nous avons jusqu’à présent toujours adopté le même principe de recherche à partir de la définition d’une mole basique correspondant à un diagramme précis dans lequel nous avons évolué par des apports conjugués de silice et d’alumine. Nous avons réduit le temps passé aux calculs et aux pesées en adoptant successivement le mélange en ligne, le mélange ternaire puis le mélange quaternaire.
Nous avons d’abord travaillé sur des pesées puis gagné encore un peu de temps et de matières premières en passant à un dosage en volume et plus précisément à un dosage en gouttes.
Je propose de conserver ce principe du dosage en gouttes sur des supports identiques, c’est-à-dire des plaquettes comprenant 36 alvéoles. Nous admettrons seulement que nous passons maintenant à une nouvelle étape et qu’après avoir trouvé une glaçure intéressante par un des procédés précédents, nous cherchons à «affiner» notre recherche par une méthode différente et complémentaire.
Cette méthode permettra à partir d’une recette de base d’étudier les apports progressifs de deux éléments pris indépendamment l’un de l’autre mais au final associés dans tous les mélanges possibles.
On fera progresser le premier élément verticalement de la première rangée jusqu’à la dernière en progressant d’une goutte à la fois. Cet apport se fera de 0 à 5 gouttes ou de 1 à 6 gouttes en progressant d’une goutte à la fois d’une rangée de 6 alvéoles à la suivante.
Le choix du départ entre 0 et 1 dépendra de l’intérêt de la présence ou non de cet élément au début de la progression. Nous verrons plus loin un exemple pratique qui sera plus parlant.
On fera progresser le deuxième élément horizontalement de la première rangée verticale à gauche jusqu’à la dernière rangée à droite en progressant toujours d’une goutte à la fois de 0 à 5 ou de 1 à 6.
Si après ces deux premiers dosages vous comptez le nombre de gouttes contenues dans chaque alvéole vous verrez que la première située dans l’angle en bas à gauche en contient de 0 à 2. Si vous prenez l’alvéole située dans l’angle en haut à droite, vous compterez de 10 à 12 gouttes. Il reste donc à compléter et à ajouter à chaque alvéole le nombre nécessaire de gouttes de l’émail de base pour avoir au final 10 ou 12 gouttes dans chaque essai.
Il faudra donc commencer le dosage par l’angle supérieur droit pour finir par l’angle inférieur gauche en progressant de 1 goutte à la fois sur les diagonales. Le dosage se fera soit de 0 à 10 gouttes soit de 1 à 11 car nous pouvons avoir des essais dosés au final soit à 10 soit à 12 gouttes.
Un exemple précis et trois petits graphiques seront plus parlants qu’un long discours. Admettons que je dispose d’un émail qui me donne un rouge de cuivre classique. Je l’ai trouvé dans un livre et j’ai suivi fidèlement la recette indiquée et celle-ci se termine par le dosage en carbonate de cuivre qui est de 1 % et par un apport d’oxyde d’étain de 3 %. Je voudrais simplement m’assurer que la teneur en carbonate de cuivre retenue est bien la meilleure et savoir s’il est vraiment nécessaire d’apporter ces 3 % d’oxyde d’étain, matière onéreuse.
Je vais préparer trois recettes :
Je dose verticalement mon émail avec carbonate de cuivre mais sans oxyde d’étain. Je commencerai à une goutte pour finir à 6. Il me faut du cuivre dès la première rangée car je sais déjà que sans cuivre la couleur ne se développera pas. La dernière rangée au final ne sera pas dosée à 2 % de carbonate de cuivre mais bien à 1 % car seules 6 gouttes sur les 12 au total contiendront du cuivre.
Je dose horizontalement mon émail avec oxyde d’étain mais sans carbonate de cuivre. Cette fois je commence à 0 goutte pour finir à 5. Rien ne prouve en effet que l’oxyde d’étain est nécessaire au développement du rouge et cette première rangée sans étain pourra peut-être me le confirmer. Là aussi la dernière rangée ne sera pas dosée à 7 % d’oxyde d’étain mais précisément à : 7 × 5/12 soit 2,9 % d’oxyde d’étain car seules 5 gouttes sur les 12 au total contiendront de l’étain.
Enfin, je complète l’ensemble des essais par un apport de l’émail de base seul en partant de l’angle supérieur droit dosé à 1 goutte pour finir à l’angle inférieur gauche dosé lui à 11 gouttes. Au final chacune des 36 alvéoles aura donc reçu 12 gouttes.
Imaginons qu’après cuisson des essais, je juge que le résultat le plus intéressant est celui dosé à 3 gouttes de l’émail de base avec oxyde de cuivre et à 4 gouttes du même émail avec oxyde d’étain. La meilleure recette sera donc dosée à :
| + |
|
Soit un émail dosé à 0,5 % de carbonate de cuivre et à 2,3 % d’oxyde d’étain.
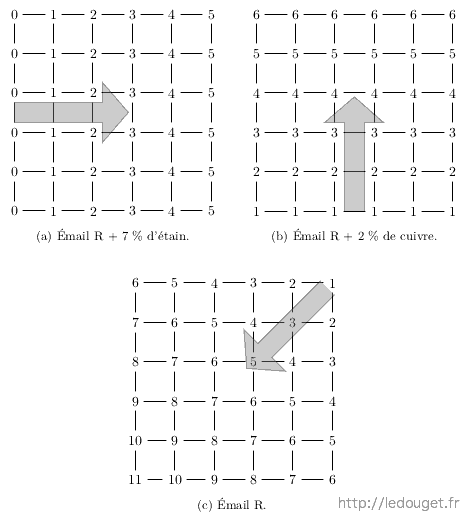
Figure 2.9: Dosage en gouttes sur plaquette à 36 essais. Exemple de progression de deux apports : cuivre et étain dans un émail de base R.
La première étape consiste à préparer une certaine quantité de l’émail de base. Tout dépendra du nombre de plaquettes envisagées. Pour la réalisation d’une seule plaquette, 30 grammes suffisent.
J’ai fait le choix du dosage en gouttes. Il est tout à fait évident que cette méthode est transposable à un dosage par pesées avec progression de 1 gramme à la fois avec utilisation de gobelets en plastique et émaillage de plaquettes à essais en L.
Même si j’ai fait allusion au cours des pages précédentes à certaines grandes familles classiques de glaçures comme le céladon, nous n’avons pour l’instant étudié les glaçures que comme des verres incolores. Aucune des matières étudiées précédemment n’est censée apporter de la couleur à l’émail même si ce n’est pas tout à fait vrai. En effet, presque toutes les matières contiennent de l’oxyde de fer, parfois en trace, souvent en forte quantité comme certaines argiles.
J’ai parlé de fer, donc d’un métal car effectivement ce sont les métaux sous forme d’oxyde ou de carbonate qui vont apporter les couleurs à l’émail. Nous allons en passer quelques-uns en revue sans avoir la prétention d’écrire un livre sur un sujet trop vaste.
Avant toute chose, sachez que plusieurs facteurs essentiels vont intervenir dans le développement de la couleur et que c’est là un immense champ de recherche pour le céramiste :
Voici un rapide tour d’horizon des métaux les plus employés et de la palette qu’ils autorisent.
A lui seul, il serait suffisant pour occuper et satisfaire les recherches d’un émailleur. D’ailleurs dans le livre de Daniel de Montmollin, il est le seul métal étudié car sa palette est immense.
Dans une base calcique ou calcique et légèrement alcaline, le fer nous donnera toute la palette des céladons. On passera du bleu pâle à 0,5 % au vert clair puis plus foncé entre 1 et 2 %, au vert olive à 3 % pour accéder au noir dès 4 % et bien au-delà.
Si la glaçure est calcique et alcaline, dans un rapport alumine / silice dominé par cette dernière , nous aurons un bleu lavande déjà simplement avec des traces de fer. La couleur prendra de l’intensité et de la profondeur en faisant progresser le fer jusqu’à 2 %. Nous sommes dans les «bleus de fer».
Avec des apports plus importants jusqu’à 10 % de fer nous obtenons des noirs et des rouges de fer. C’est souvent le même émail qui nous fera passer du rouge au noir en jouant sur l’épaisseur de celui-ci. Vous en avez des exemples intéressants dans le livre consacré à Robert Deblander aux pages 78, 81 et 82 (voir bibliographie p. ??).
Dans les glaçures très alcalines (proches donc du diagramme n°60) et fortement alumineuses, une faible quantité de fer autour de 1 % sera suffisante pour obtenir ce qu’on appelle un «shino rouge», une couleur qui ira du «saumon» pâle à un rouge «rouille» soutenu, là aussi souvent en fonction de l’épaisseur de l’émail.
En recherchant autour du diagramme n°43 de Daniel de Montmollin on peut développer des glaçures de type «gouttes d’huile». Le fer se situe autour de 7 à 8 %. Sans en reprendre la description déjà faite dans cet ouvrage, je voudrais juste souligner que c’est la réduction du fer en fin de cuisson qui produit le phénomène. Passé 1200 °C, le fer devient instable et sa réduction s’opère simplement du fait de la température atteinte et non par l’action d’un agent réducteur comme le carbone. Le fer libère son oxygène de plus en plus facilement en passant par des formes de moins en moins oxydées. Dans l’oxyde ferrique Fe2O3, la part d’oxygène est de 30 %, dans l’oxyde magnétique Fe3O4, elle est de 27,6 % et elle n’est plus que de 22,2 % dans l’oxyde ferreux FeO. Pour que ce phénomène se produise en fin de cuisson, il ne faut donc pas que cette réduction se fasse précédemment à 900 ou 1000 °C pour que le fer conserve son oxygène à cette basse température pour pouvoir le perdre plus tard. Il nous faut donc bien cuire ce type de glaçure en atmosphère oxydante.
Celle-ci favorise également une autre glaçure riche en fer qui donne une teinte rouille très vive que l’on nomme Kaki par comparaison avec la couleur du fruit du même nom. Il s’agit d’un rouge de fer un peu particulier puisqu’il demande la présence d’une petite quantité de phosphore pour qu’apparaisse cette couleur de surface due à un phosphate de fer. On intègre 0,1 P2O5 dans la formule unité de l’émail apporté généralement par la cendre d’os. Le diagramme 27 est une bonne base de départ.
En réduction, le cuivre utilisé souvent sous forme de carbonate permet d’obtenir ce rouge mythique que les Européens envièrent aux Chinois pendant des siècles avant d’en percer le secret. C’est le fameux rouge sang connu sous le nom de «Sang de bœuf». Les variantes et les appellations poétiques sont nombreuses.
Une faible quantité de cuivre est suffisante, autour de 0,5 %. On y ajoute souvent une petite quantité d’oxyde d’étain, en intégrant parfois baryum ou bore dans la formule unité. On peut démarrer une recherche dans la zone proche du diagramme 25 en choisissant plutôt un feldspath sodique. Il faut éviter une réduction forte qui nuit au développement de la couleur.
Moins connu et pourtant dans une base identique, on peut trouver des teintes pourpres, violines en favorisant la silice dans le rapport alumine/silice. Nous sommes exactement dans une zone favorable aux bleus de fer et il n’est pas incongru de penser que des traces de fer dans l’émail seraient suffisantes pour développer ce bleu qui viendrait se mêler au rouge et donner cette teinte violacée.
En oxydation, c’est encore dans cette même zone que nous trouverons des bleus et il suffira d’augmenter l’alumine tout en diminuant la silice pour voir la teinte passer au vert. Les plus belles de ces glaçures peuvent soutenir la comparaison avec les céladons. D’ailleurs, on trouve parfois l’expression "céladon de cuivre" dans des vieux ouvrages de technologie céramique.
Les bleus de cuivre ne sont donc pas l’apanage des glaçures riches en baryum même s’il est vrai que celles-ci favorisent le bleu quels que soient les rapports alumine/silice.
En oxydation toujours, le cuivre autorise aussi une couleur orange dans les glaçures très alcalines et fortement alumineuses.
Au final, le cuivre est un bel exemple pour illustrer le rôle des nombreux facteurs dans le développement des couleurs : le métal, les atmosphères de cuisson, la nature de l’émail et tout aussi déterminants, les rapports alumine/silice dans la glaçure.
Le plus souvent utilisé sous forme de carbonate, il donne presque exclusivement du bleu et cela que l’atmosphère soit oxydante ou réductrice. Son pouvoir colorant est très fort et un faible pourcentage suffit à développer une couleur dense. Il est possible de trouver toutes les nuances en fonction de la glaçure choisie et de la nature de sa mole basique. Là encore, il faudra trouver le meilleur rapport alumine/silice.
Je connais au moins une exception au bleu, c’est le vert soutenu que le cobalt développe quand il est associé au titane dans des glaçures très alcalines.
Son pouvoir colorant ne s’exerce vraiment qu’en atmosphère oxydante. Peu employé, je me souviens en avoir tiré un rose un peu violine que je posais sur porcelaine. Il est souvent associé au fer et au cobalt pour donner des noirs.
Il peut donner un vert assez violent et peu nuancé dans la plupart des glaçures que ce soit en atmosphère oxydante ou réductrice. Il y a au moins deux exceptions à cela dans des glaçures dont la mole basique est riche en magnésium ou en zinc. Cela peut être le cas dans une glaçure magnésienne type du diagramme n°39 ou le chrome développe alors une teinte rose saumon.
Le nickel est souvent délaissé par les céramistes car la palette qu’il offre en réduction est assez terne et peu intéressante. Par contre en oxydation, il permet de développer une gamme étendue de couleurs assez vives en fonction là aussi de la famille des glaçures retenues. J’ai obtenu des verts-jaunes dans des bases des diagrammes 21 et 43, ainsi que du jaune quand le nickel est associé au titane. Je sais qu’il permet des bleus et même des rouges. C’est un oxyde qui mériterait une recherche approfondie par ceux qui ont fait le choix de la cuisson oxydante.
Le champ de recherche est déjà suffisamment vaste avec ces quelques matières abordées pour ne pas m’étendre sur l’utilisation de certains oxydes rares ou peu employés comme le vanadium, le strontium, cadmium et autre sélénium. Sachez simplement que les fournisseurs proposent également quelques minerais peu onéreux dans lesquels on trouve de l’oxyde de fer associé au titane comme dans le rutile ou l’ilménite ou associé au chrome comme dans le chromate de fer.
Tout comme dans le livre écrit par Daniel de Montmollin, j’ai fait le choix de limiter le nombre des éléments retenus pour la réalisation des glaçures. Pour que la démonstration et les calculs paraissent les plus clairs et les plus compréhensibles, il faut en effet éviter de se noyer sous une masse d’informations.
Nous n’avons donc retenu dans la mole basique que quatre oxydes : le calcium, le magnésium et réunis sous une même appellation, le sodium et le potassium. Ce sont les trois sommets du triangle des 60 diagrammes proposés. Le jour où l’envie vous prendra d’ «explorer des terres nouvelles», vous pourrez les aborder en intégrant dans la colonne basique d’autres oxydes.
L’oxyde de baryum BaO dont la masse molaire est 153. Il est introduit dans l’émail par le carbonate de baryum BaCO3 dont la masse molaire est 197. On connaît son point eutectique : BaO 0,43 Al2O3 4 SiO2 qui fond à 1200 °C. Prudence cependant car il faut savoir que le carbonate de baryum est un poison et qu’on doit donc le manier avec précaution. Il n’est pas non plus conseillé d’utiliser des glaçures fortement dosées en baryum pour une production à usage alimentaire.
L’oxyde de zinc ZnO que l’on trouve sous cette forme chez les fournisseurs. Sa masse molaire est 81.
L’oxyde borique B2O3 de masse molaire 70 qui est apporté dans l’émail par l’emploi de frittes du commerce. Les fournisseurs indiquent leur composition et leur masse molaire, ce qui permet de les intégrer dans le calcul d’un émail comme toute autre matière. Il existe pourtant une matière naturelle qui contient du bore sous forme insoluble, c’est la colémanite mais celle-ci a le grand désavantage d’être fortement hydratée et de provoquer bouillonnements, défauts et décollements dans les glaçures.
Traditionnellement, B2O3 n’est pas classé dans la colonne des oxydes basiques mais dans celle de l’oxyde amphotère Al2O3. C’est Marc Uzan qui en a fait la proposition dans ce qu’il appelle la Formule Molaire Extensive (F.M.E.). Vous en lirez l’explication dans son livre (voir bibliographie p. ??). Vous y trouverez aussi tout un champ d’explorations possibles pour des glaçures dont les moles basiques intègrent aux côtés de CaO et KNaO, BaO, ZnO et B2O3.
L’oxyde phosphorique P2O5 qui est considéré, ainsi que le bore, comme étant formateur de verre. Il est apporté dans la glaçure soit par les cendres où il est parfois fortement concentré ou par la cendre d’os où il est associé à la chaux sous forme de phosphate de chaux de formule 3 CaO P2O5 masse molaire 310. C’est encore Daniel de Montmollin qui a su démontrer son importance dans la mise au point des glaçures à «nucléations» ou dans le développement de certaines couleurs comme ce rouge de fer au phosphore que l’on nomme «kaki».
Le titane TiO2 que l’on devrait classer dans la colonne acide en compagnie de la silice. Son rôle est mal défini. On sait qu’il influence le développement des couleurs associé à d’autres oxydes, parfois en bien, parfois en mal quand il donne aux céladons une teinte jaunâtre. Il n’est pas censé être un oxyde colorant et pourtant on lui doit des jaunes dans les glaçures très alcalines ainsi que des bleus.
L’oxyde d’étain SnO2 que l’on désigne dans tous les ouvrages comme «opacifiant». Il faut savoir que ce n’est vrai qu’en atmosphère oxydante. Généralement on évite d’employer en forte quantité cette matière onéreuse. On trouve souvent un petit pourcentage d’oxyde d’étain dans les rouges de cuivre. On l’utilise aussi associé au chrome pour développer les fameux roses et rouges de chrome.
Là non plus, il n’est pas question de reprendre en détail ce qui a déjà été si bien étudié et écrit par Daniel De Montmollin (voir bibliographie p. ??).
Je voudrais juste faire le parallèle entre le matériau cendre et nos glaçures. Nous retrouvons dans la formule d’une cendre les oxydes empruntés au sol et à la roche par la plante et qui nous sont restitués après calcination de celle-ci.
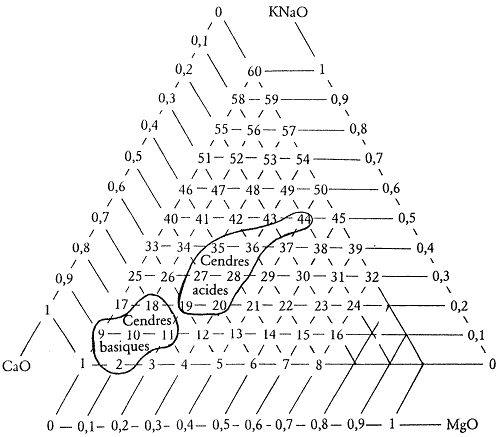
Figure 4.1: Répartition des cendres dans les 60 diagrammes de Daniel de Montmollin.
Ces oxydes sont les mêmes que ceux que nous avons déjà abordés et si nous connaissons l’analyse de la cendre nous pouvons en établir la formule unité et la répartir de la même façon en trois colonnes :
nous y retrouvons CaO, MgO, Na2O et K2O associés dans des proportions diverses. Voici dans les diagrammes déjà étudiés (cf. figure 4.1), ceux dans lesquels on peut retrouver les différentes familles de cendres. Les cendres de bois sont très proches du sommet CaO. Les cendres de paille et de graminées sont plus alcalines et magnésiennes.
la plupart des cendres ne contiennent qu’une très faible quantité d’alumine. Il y a cependant une exception : ce sont les cendres de vigne qui affichent de 0,15 à 0,3 Al2O3 dans la formule unité.
il faut distinguer ici trois familles de cendres. Les cendres dites basiques qui sont données par les bois sont très pauvres en silice. Les cendres acides comme les cendres de paille au contraire en contiennent des quantités importantes, parfois plus de 5 SiO2 dans la formule. Il existe des compositions intermédiaires pour des cendres que Daniel de Montmollin nomme «mixtes».
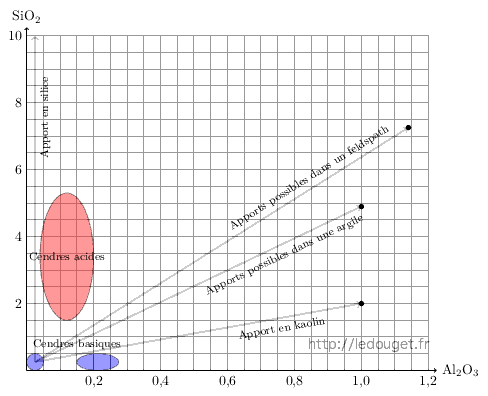
Figure 4.2: Positions des cendres dans le diagramme.
On dispose donc de tous les éléments nécessaires pour faire figurer nos différentes cendres dans un diagramme de fusion et visionner ainsi quels sont les éléments susceptibles d’être apportés aux cendres pour en faire des glaçures exploitables. Je ne présente qu’un diagramme mais il ne faut pas oublier qu’il faudrait autant de diagrammes de fusion qu’il y a de moles basiques différentes dans les formules de cendres. Nous pouvons être dans le diagramme n°2 ou dans le n°44, c’est la cendre qui commande.
Nous voyons qu’en faisant figurer les compositions de cendre dans ce diagramme, on comprend immédiatement quels sont les apports que nous pourrons faire en silice et en alumine pour ajouter à la cendre les éléments qui lui manquent pour former une glaçure. Nous pouvons apporter quartz, kaolin, argiles diverses et aussi associer cendre et feldspath en sachant alors que les différents mélanges nous feront «sauter» d’un diagramme à l’autre. Ce qu’il ne faut pas oublier, c’est que la cendre est une matière spécifique et que si nous lui ajoutons une trop grande quantité d’autres éléments nous risquons de lui faire perdre cette spécificité pour en faire une matière ordinaire sans grand intérêt.
Nous savons que la particularité des cendres est d’apporter dans l’émail du phosphore. Celui-ci doit donc rester en quantité significative pour influer sur l’aspect des glaçures.
Nous avons déjà eu souvent l’occasion d’utiliser une argile dans la réalisation des glaçures même si celle-ci est un peu particulière puisqu’il s’agit d’une argile pure dite «primaire» : le kaolin.
Pourquoi ne pas utiliser également d’autres argiles dites «secondaires» puisque nous en disposons d’au moins une, l’argile à grès qui nous sert à réaliser nos poteries ?
Nous savons que le kaolin nous apporte alumine et silice, notre argile à grès le fera également mais dans un rapport différent. Elle apportera en plus de façon significative un certain pourcentage de fer. Il faudra donc que ce fer soit le bienvenu dans le type de glaçure recherchée. Il faudra encore que nous disposions de la composition et de l’analyse de cette argile pour pouvoir en calculer la formule et l’intégrer ainsi dans le calcul de l’émail. Il n’est pas difficile d’obtenir auprès des fournisseurs l’analyse des argiles. En voici un exemple : il s’agit de la terre à grès de Saint-Amand fournie par les établissements Solargil sous l’appellation GSA. Son analyse chimique est la suivante :
| SiO2 | 62,40 % | CaO | 0,20 % |
| Al2O3 | 21,65 % | MgO | 0,20 % |
| TiO2 | 0,40 % | K2O | 2,40 % |
| Fe2O3 | 2,10 % | Na2O | 0,30 % |
| P.F. | 7,06 % | ||
| Total | 96,71 % |
Nous procédons de la même façon que pour toute autre matière pour passer de l’analyse à la formule. Nous l’avons déjà fait pour le feldspath potassique. Nous retenons les éléments significatifs et les divisons par les masses molaires correspondantes. Nous obtenons une formule provisoire. La seule différence pour passer de la formule provisoire à la formule définitive, c’est que cette fois-ci nous ferons le choix de ramener Al2O3 à 1 et non pas l’élément basique. Une argile n’est pas une matière basique même si ici la teneur en K2O n’est pas négligeable. Le diviseur commun sera donc la valeur trouvée pour Al2O3 dans la formule provisoire. Nous obtenons la formule définitive : Al2O3 4,9 SiO2.
Nous pouvons d’ailleurs ne pas négliger K2O et l’intégrer dans le calcul. Dans ce cas nous arriverons à la formule : 0,12 K2O Al2O3 4,9 SiO2, et sans jamais oublier que l’argile nous apporte aussi 2 % d’oxyde de fer.
Cette analyse est celle d’une argile crue. Sa masse molaire est calculée en divisant le total de l’analyse, 96,71, par le même diviseur commun. Nous obtenons 456. Si nous voulons connaître la masse molaire de l’argile calcinée il suffira de refaire le calcul en retranchant la perte au feu du total de l’analyse et nous obtiendrons une masse molaire de 422. A l’usage, comme on associe le plus souvent dans l’émail une part d’argile crue et une part d’argile calcinée, il faudrait théoriquement tenir compte des deux valeurs de la masse molaire.
Connaissant le rapport alumine/silice de notre argile GSA on peut faire figurer sur un diagramme de fusion la progression des apports de cette argile. Je reprends l’exemple du diagramme calcique n°1.
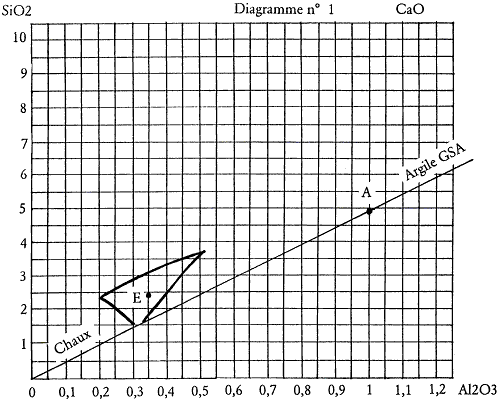
Figure 4.3: Mélanges chaux-argile dans le diagramme n°1.
Le point A tracé à l’intersection Al2O3 4,9 SiO2 indique qu’à ce point précis correspondra une recette composée d’une mole d’argile et d’une mole de carbonate de chaux. La droite partant du point 0 et passant par ce point permet de représenter tous les mélanges possibles entre d’un côté la chaux et de l’autre l’argile. Nous pouvons calculer la recette correspond à ce point A :
| Argile GSA | 1 × 456 | = | 456 | : | 556 × 100 = 82 |
| Carbonate de chaux | 1 × 100 | = | 100 | : | 556 × 100 = 18 |
| 556 |
Nous voyons que notre recherche pourra éventuellement se poursuivre à droite de ce point A et que sur la gauche il existe bien d’autres possibilités au moins jusqu’à 1,5 moles de silice. On considère qu’en dessous de cette valeur, l’émail serait trop pauvre en silice pour être suffisamment stable et résistant à l’usure. A partir de chaque point de cet axe on peut également faire un apport de quartz et établir au choix mélanges ternaires et quaternaires.
Nous avons choisi de figurer le mélange chaux et argile or il se trouve que la nature y a pensé avant nous. Ce sont les marnes et les argiles marneuses qui sont parfois sans modification des glaçures en «puissance».
Nous aurions pu de la même façon faire figurer sur un autre diagramme les mélanges possibles entre cendre et argile.
Dans le diagramme 4.4 qui reprend l’exemple de notre recherche dans cette base n°33, une droite représente notre apport d’argile à partir du point A, à comparer avec l’apport de kaolin le long de la droite AC.
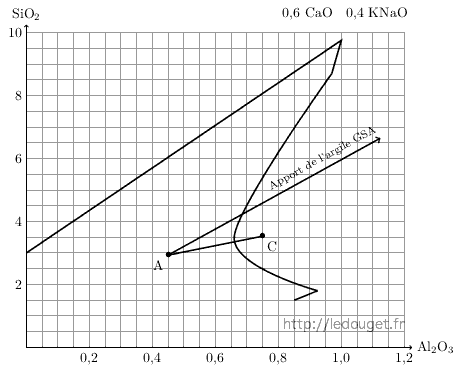
Figure 4.4: Diagramme n°33.
L’utilisation d’une argile rouge très riche en fer permettra de trouver des glaçures noires sans apport d’oxyde de fer supplémentaire, simplement par mélange de cendre et d’argile ou de chaux et d’argile. J’utilise personnellement une argile de Noron-la-Poterie en Normandie de formule : Al2O3 5,4 SiO2 masse molaire 507. Elle contient de 6 à 8 % d’oxyde de fer. Elle est vendue en poudre, ce qui est bien pratique. Pour d’autres argiles, je récupère la poussière résultant du ponçage des pièces réalisées à la plaque. Je calcine l’argile en four à dégourdi mais je conserve dans mes bains d’émail au moins 10 % d’argile crue.
Chacun dans sa région peut au cours de ses promenades repérer des carrières en exploitation et se procurer ainsi à moindres frais des matières premières bien spécifiques qui ne figureront jamais dans les catalogues des fournisseurs. En prenant contact poliment avec le propriétaire ou l’exploitant de la carrière, vous obtiendrez sûrement l’autorisation de récupérer quelques sacs de poussière auprès des concasseurs. Vous aurez peut-être même la chance de disposer de la nature et de l’analyse de la roche exploitée. CaO C’est ainsi qu’un ami m’a procuré quelques kilos d’une poussière de roche provenant de la carrière de la Pommeraie près de Nantes. Il avait obtenu également la composition chimique en pourcentage de cette roche nommée Orthogneiss. La voici :
| SiO2 | 70,0 % | CaO | 1,4 % |
| Al2O3 | 14,0 % | MgO | 1,6 % |
| Fe2O3 | 3,8 % | Na2O | 4,2 % |
| TiO2 | 0,4 % | K2O | 4,5 % |
On procède comme nous l’avons déjà fait pour le feldspath et l’argile pour calculer la formule de notre roche. Après calcul et formule provisoire nous obtenons la formule définitive suivante :
| 0,14 CaO 0,76 Al2O3 6,48 SiO2 | masse molaire 555 |
| 0,22 MgO | |
| 0,64 KNaO | sans oublier 3,8 % d’oxyde de fer |
La formule de la mole basique va nous permettre de situer cette roche dans le triangle des 60 diagrammes de Daniel de Montmollin. Nous voyons qu’elle se trouve en dessous du diagramme n°53, légèrement au-dessus et entre les diagrammes n°48 et 49.
Si nous prenons un de ces trois diagrammes pour y reporter les quantités moléculaires d’Al2O3 et de SiO2 nous voyons que cette roche se situe en plein cœur de la zone de fusion définie par Daniel de Montmollin. Il s’agit donc d’une glaçure «en puissance» dans une zone encore favorable aux émaux à «gouttes d’huile». Il suffirait sans doute d’apporter un peu de fer supplémentaire à cette roche pour obtenir un émail de ce type.
N’oublions pas que c’est une roche de rencontre qui fit redécouvrir à frère Daniel le secret perdu de ces glaçures au fer. Plus modestement, c’est aussi en faisant un apport de dolomie dans cette roche orthogneiss que j’ai trouvé un joli jaune de fer qu’il m’a été possible par la suite de reconstituer dans le diagramme 21 une fois ma réserve de poussière de roche épuisée.
Si on ne veut pas se contenter du seul hasard des promenades pour découvrir de nouvelles matières premières, on peut plus rationnellement et plus efficacement se procurer la carte géologique de sa région au 1/50 000. Ces cartes sont établies par le Bureau de Recherches Géologiques et Minières (BRGM) et on peut se les procurer auprès des éditions du BRGM, 3 avenue Claude Guillemin BP. 36009 — 45060 Orléans Cedex 2. Tél. 02 38 64 34 34. ou plus simplement sur leur site internet : http://www.brgm.fr/cartegeol.jsp
Ces cartes sont très détaillées, on y trouve outre la nature des sols, des foules de renseignements dont bien sûr l’emplacement des carrières. Chaque carte est accompagnée d’un livret explicatif sur la nature des sols avec de très nombreuses analyses chimiques des roches rencontrées.
A partir du livret accompagnant la carte géologique «Pont-Croix, baie d’Audierne» dans mon coin de Bretagne, je m’étais «amusé» à calculer les formules des différents types de roches. La figure 4.5 montre où elles se situent sur le triangle CaO KNaO MgO des 60 diagrammes de Daniel de Montmollin.
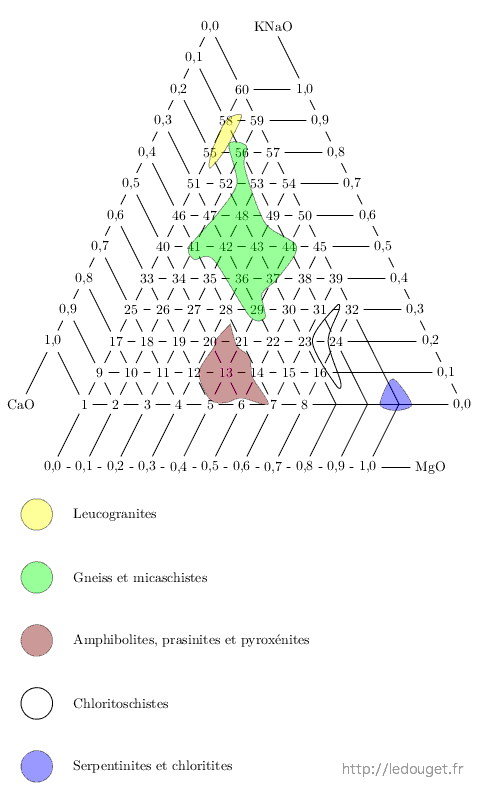
Figure 4.5: Sur le triangle CaO KNaO MGO des 60 diagrammes de Daniel de Montmollin, positionnement des différents types de roches.
J’ai fait le choix d’un four en 1977 et aujourd’hui je l’utilise toujours. On admettra donc que mon expérience est longue mais qu’elle est aussi limitée.
C’est un four Chapin en briques légères de 500 litres de volume utile doté de chaque côté d’une rampe composée de quatre brûleurs à air induit. Il n’y a pas plus simple dans le principe que ce modèle puisque le gaz arrive sous pression au cœur du brûleur et que le mélange air/gaz se fait par le réglage d’une bague qui contrôle le volume d’air aspiré dans le brûleur : c’est l’air «primaire».
On trouve au-dessus de chaque brûleur un orifice dont l’ouverture peut être modifiée par une glissière en métal qui coulisse au-dessus des brûleurs des deux côtés du four. Le réglage de ces glissières permet de régler un apport d’air que l’on appelle «secondaire» et qui vient si nécessaire en complément de l’air primaire.
Deux plaques en béton réfractaire coulissent à l’arrière du four et viennent obstruer plus ou moins le conduit de cheminée. C’est ce qu’on appelle le registre. Dans mon four, en position de plus grande fermeture, le passage de la cheminée fait encore 20 cm de côté.
Je n’ai pas l’intention de vous abreuver de formules compliquées piquées ici et là dans les livres techniques mais d’aborder le sujet en termes simples. Nous pourrons mener des cuissons en atmosphère oxydante ou en atmosphère réductrice. Pour ce qui est de la cuisson neutre, on peut au mieux chercher à s’en approcher.
Dans la cuisson oxydante, la combustion est totale et donc la production de chaleur optimale mais il est mis en présence du combustible plus d’air qu’il n’est nécessaire pour obtenir cette combustion. Nous sommes donc en excès d’air. Si cet excès d’air est suffisant, nous pourrons obtenir en four à gaz une palette de glaçures comparable à celle que l’on obtiendrait en four électrique. Là, je suis dans la théorie puisque je n’ai jamais cuit en four électrique. Ce serait un sujet de recherche et une comparaison intéressante à entreprendre. Des analyses que j’ai pu réaliser au cours de quelques cuissons, il semble bien qu’il ne faille jamais descendre en dessous des 3 % d’oxygène dans les gaz de combustion pour mener à bien ce genre de cuisson. Je me souviens avoir lu un texte d’Antoine d’Albis qui préconisait 5 % d’oxygène.
Dans une cuisson réductrice, la quantité d’air mise en présence du combustible sera inférieure à la quantité nécessaire pour obtenir une combustion complète. Le carbone ne trouvera pas assez de molécules d’oxygène pour se combiner et former du CO2. Le taux de gaz carbonique va diminuer dans le four au profit du monoxyde de carbone CO qui lui augmentera au fur et à mesure que CO2 diminuera. C’est en-dessous de 13,8 % de CO2 que CO commence à se former et plus ce taux diminuera plus la réduction sera forte. CO étant instable, il n’aura de cesse de trouver le O qui lui manque pour devenir CO2. Ne trouvant pas O dans l’atmosphère du four, il ira le chercher dans les oxydes métalliques au cœur des émaux. On lui devra alors céladons et autres rouges de cuivre. Personnellement, je n’ai jamais jugé utile de descendre en dessous de 12 % de CO2, ce qui correspond à une réduction légère. Théoriquement le taux d’oxygène devrait se tenir à 0 % dans les gaz de combustion.
La combustion neutre est celle dans laquelle l’air est apporté en quantité juste nécessaire pour assurer une combustion complète et rien de plus. On ne doit pas avoir d’excès d’air et le taux de CO2 doit être le plus proche de 13,8 %. C’est la combustion idéale vers laquelle il faut tendre lorsque au-delà d’une certaine température la présence de CO ne s’impose plus même dans une cuisson réductrice.
En titre, j’ai parlé de trois combustions. En réalité on peut y ajouter une quatrième que l’on nomme «oxydo-réduction». C’est un cas de figure particulier dans lequel on se trouve avoir en même temps un excès d’air et donc présence d’oxygène dans les gaz de combustion mais aussi formation de monoxyde de carbone. C’est théoriquement un défaut de réglage à éviter. Personnellement, je me suis rendu compte qu’en cuisant en réduction légère, une partie de mon four était sortie oxydante en raison d’une entrée d’air parasite provoquée par une mauvaise étanchéité de la porte sur un côté. Je conserve souvent cette façon de cuire car elle me permet de doubler mes essais, les uns en oxydation, les autres en réduction. A la frontière des deux zones, je peux aussi obtenir des effets intéressants d’une seule et même glaçure développant deux couleurs sur la même pièce.
En début de cuisson, la conduite à tenir sera la même quelle que soit l’atmosphère choisie. A faible pression, les brûleurs sont réglés pour présenter une flamme bien bleue avec le minimum de ces imbrûlés qui composent le panache orange en bout de flamme. Avec des brûleurs à air induit nous sommes dans une combustion à fort excès d’air. C’est ce qui convient en début de cuisson pour assurer une bonne ventilation du four et le dégagement de la vapeur d’eau provenant des émaux.
Pour monter en température, il faut augmenter la pression donc la quantité de gaz. La quantité d’air primaire aux brûleurs ne change pas et la combustion devient plus efficace au fur et à mesure que l’excès d’air diminue. Il arrive un moment où on approche de la combustion neutre et puis la quantité de gaz augmentant encore sans apport d’air supplémentaire on passe alors en atmosphère réductrice.
D’après mes observations, mon four a alors atteint les 900 °C. Si je désire cuire en atmosphère réductrice, je ne change rien encore aux réglages. Par contre si je fais le choix d’une cuisson oxydante, il est urgent d’apporter de l’air aux brûleurs. Comme il n’est pas possible d’augmenter la quantité d’air primaire, j’ouvre légèrement, en faisant coulisser une glissière, les ouvertures au-dessus des brûleurs qui laissent pénétrer l’air secondaire. A moi de trouver le bon réglage pour que cette quantité d’air soit suffisante mais pas en excès. Elle ralentirait alors la montée en température.
Si j’ai fait le choix de la cuisson réductrice, j’attendrai d’avoir atteint les 1000 °C pour faire un léger apport d’air secondaire et éviter ainsi que la réduction ne devienne trop forte. De grandes flammes qui brûlent dans le cheminée à la sortie du registre prouvent bien sûr une atmosphère réductrice mais surtout un gaspillage de gaz. Je règle mon apport d’air secondaire en conséquence pour éviter ces flammes au registre. En maintenant un taux de CO2 proche des 12 %, je sais avoir entre 0,5 et 1 % de CO, ce qui me paraît suffisant.
Du jour où j’ai pu faire mes premières analyses, je me suis rendu compte que je finissais mes cuissons avec des taux de 4 à 5 % de CO. Depuis, mes cuissons réductrices ne durent plus 14 mais 12 heures.
D’après mes observations et pour avoir eu souvent l’occasion de passer d’une combustion à une autre, j’ai la quasi-certitude que l’essentiel se joue tôt dans la cuisson, entre 800 °C et 1000 °C. Vouloir réduire avant serait inutile et source de gaspillage et démarrer une réduction après, sans doute trop tard.
Il y a deux facteurs qui interviennent, c’est d’une part la température qui est alors suffisante pour permettre à CO d’atteindre une grande efficacité, son «avidité» pour l’oxygène augmentant en même temps que la température. Il se trouve qu’au même moment, tous les autres oxydes voient au contraire leur liaison avec l’oxygène s’affaiblir considérablement. Nous avons donc d’un côté un CO de plus en plus efficace, de l’autre côté des oxydes abandonnant leur oxygène de plus en plus facilement. Le regretté Marc Feller m’avait montré à ce sujet un graphique tout à fait révélateur indiquant «l’affinité standard des éléments pour l’oxygène.»
On peut m’objecter que le phénomène se poursuivra bien plus encore au-delà des 1000 °C. C’est là qu’intervient le deuxième facteur : la porosité. Entre 800 et 900 °C, la porosité du tesson est à son maximum et la glaçure n’est pas encore entrée en fusion. Email et tesson sont alors totalement perméables aux gaz réducteurs. Plus tard, le tesson se fermera et la glaçure fondue deviendra imperméable aux gaz. Ce fait est souligné par de très nombreux auteurs. Je reprendrai juste le texte de Gréber dans son traité céramique (page 531, voir bibliographie p. ??) : «Il faut remarquer que l’atmosphère n’a d’influence sur la coloration de la masse que tant que celle-ci reste poreuse. Si le produit est recouvert d’une glaçure, l’action de l’atmosphère cesse au moment où la glaçure rentre en fusion.»
La température de 1000 °C franchie, on peut à mon idée essayer de s’approcher de la cuisson neutre ou du moins se contenter d’une faible réduction afin de monter en température avec le meilleur rendement possible jusqu’à la fin de la cuisson.
Il serait faux de croire que tout est joué une fois la température atteinte et le four éteint, même si on fait le choix de ne plus intervenir. En effet la qualité de l’émail dépendra de la vitesse du refroidissement. Un refroidissement lent entraînera dans les glaçures une légère recristallisation qui jouera sur l’aspect et la transparence de l’émail. Cette vérité est devenue évidente le jour où l’emploi de matériaux nouveaux comme la fibre céramique nous a donné des fours à refroidissement rapide et montré des glaçures translucides et excessivement brillantes.
La pratique des paliers en refroidissement est utilisée dans le cas des émaux à cristallisations mais pas seulement. Le céramiste américain Hank Murrow écrit avoir obtenu des shinos rouge sang en réalisant au refroidissement un palier oxydant de 5 heures à 1160 °C.
Il y a là tout un domaine de recherche encore bien peu exploré. Alain Valtat dans un travail sur les glaçures au cuivre montre que la couleur rouge de l’émail n’apparaît que vers 900 °C au refroidissement pour ne plus évoluer. Un échantillon retiré à 1000 °C et refroidi brusquement reste noir.
Enfin sachez qu’un émail n’est véritablement «fixé» qu’en dessous de 230 °C car à cette température il y a encore modification de volume dans l’émail du fait de la silice, c’est le «point cristobalite». Un courant d’air froid au cours d’un défournement prématuré peut alors provoquer la cassure d’une pièce.
On trouve maintenant des analyseurs en continu qui vous permettent de savoir instantanément dans quelle atmosphère se trouve votre four. Je voudrais tout de même dire quelques mots sur le matériel et le procédé d’analyse que j’ai utilisé pour comprendre et essayer d’étalonner mon four.
Figure 5.1: Diagramme de combustion propane, pour constante d’équilibre à 900 °C.
Il s’agit de deux analyseurs de type Fyrite, l’un pour l’oxygène, l’autre pour le gaz carbonique. Ces instruments contiennent chacun un liquide spécifique. A l’aide d’une sonde reliée à une poire, on pompe les gaz de combustion dans le conduit de la cheminée et on introduit ces gaz dans l’analyseur par une valve de connexion. On oblige les gaz à traverser et à bien imprégner ce liquide en retournant plusieurs fois le Fyrite. On peut alors lire sur une échelle graduée le taux de O2 ou celui de CO2. On reporte les résultats sur un graphique pour interpréter l’atmosphère présente dans le four au moment de la prise d’échantillon.
La figure 5.1 présente un modèle de ce graphique établi pour 900 °C et quelques exemples de mesures et de leur interprétation.
Nous sommes en combustion réductrice (en rose) à chaque fois que le taux de CO2 est inférieur à 13,8 % avec 0 % de O2.
Il existe différentes recettes pour engober et protéger ainsi les plaques d’enfournement contre les coulures d’émail. Personnellement je mélange pour moitié silice et kaolin, plus précisément 40 de molochite, 10 de kaolin pour 50 de silice. Le mélange est dilué à consistance de l’émail et je pose ce revêtement au pistolet en quatre passages croisés. Il est préférable de pouvoir le faire en extérieur, la plaque posée à plat sur une bassine de grand diamètre, les coins de la plaque portant sur le rebord de celle-ci.
Ce revêtement se décroche normalement très facilement et on peut l’enlever à l’aide d’une spatule métallique et d’un maillet. Il est important d’avoir toujours une surface bien plane pour support surtout s’il s’agit de formes ouvertes. Il faut savoir en effet qu’à haute température le fond de la pièce épousera la forme du revêtement. Si celui-ci est bosselé, le pied se déformera et les poteries seront bancales ou ovalisées s’il s’agit de coupes.
Si le revêtement est même légèrement abîmé, je le change. S’il est intact, je remets une couche fine d’engobe cru car j’ai remarqué qu’à la recuisson un revêtement déjà cuit pouvait s’écailler et des petits morceaux être entraînés dans le four. Je vous laisse imaginer un bout de revêtement de plaque collé en plein milieu d’un plat émaillé.
On n’engobe que la face supérieure de la plaque. Cela paraît évident mais comme je sais que le contraire s’est déjà produit, je me permets de le dire. A ce propos, il faudra penser tout de même à bien brosser le dessous des plaques au moment de l’enfournement ainsi qu’à passer l’aspirateur muni d’une brosse sous la voûte du four si celle-ci est montée en briques réfractaires.
Disposant d’une certaine quantité de pièces dégourdies, connaissant les dimensions du four, la hauteur de mes piliers, il est judicieux de prévoir un plan précis d’enfournement avant même de commencer le moindre émaillage. Cela peut se justifier pour plusieurs raisons.
Il ne sert à rien en effet d’émailler des pièces en trop qui resteront encombrer les étagères jusqu’à la cuisson suivante en prenant la poussière. De plus, imaginons qu’un émail se soit montré décevant et que l’on s’aperçoive alors qu’il en reste plusieurs émaillées ainsi sur l’étagère, il faudra alors enlever l’émail et laver les pièces. C’est une perte de temps et de matière.
Enfournant au jugé, imaginons maintenant qu’il vous manque 1 ou 2 cm pour mettre en place la dernière pièce en haut de four. Vous voilà défaisant et défournant pour trouver une meilleure solution.
Enfin, ayant acquis une bonne connaissance de votre four, vous remarquerez des variations importantes d’une zone à l’autre, que ce soit au niveau de la température ou aussi au niveau des atmosphères de cuisson. Alors, il ne sera plus question d’émailler au hasard et le choix de l’émail sera fonction de l’emplacement de la pièce dans le four.
On établit donc un plan d’enfournement sur papier sur lequel on dessine sommairement l’emplacement des pièces et la hauteur des piliers. On repère également la hauteur des plaques par rapport à la sole.
On prépare pour chaque pièce une fiche (un quart de format A4) sur laquelle on indiquera la nature de la pièce, la description de l’émaillage avec références de ou des émaux choisis et enfin l’emplacement retenu dans le four. Quand ceci a été fait pour l’ensemble des pièces, l’émaillage peut commencer.
Cette fiche restera sous la pièce à émailler durant toute la période d’émaillage. Dans mon cas, cela dure parfois plus de huit jours et il faut savoir que lorsqu’on superpose jusqu’à trois émaux différents sur une même pièce, il peut se passer plusieurs jours entre la pose de la première couche et la pose de la dernière. Vous comprendrez l’intérêt d’avoir sous les yeux ces indications écrites car il est impossible de tout mémoriser. Une croix au feutre de couleur bien visible me permet de signaler les pièces achevées et de contrôler rapidement avant enfournement que l’émaillage est bien terminé.
Au moment de l’enfournement, je trace sur la fiche un petit schéma simplifié qui me permet de localiser précisément la pièce sur la plaque d’enfournement. Après cuisson, au moment du défournement, il faudra en effet que chaque pièce retrouve sa fiche, que ce soit une réussite ou un ratage total. Je dirais même surtout si la pièce est ratée car une réussite est la confirmation de ce que l’on a déjà compris alors qu’il reste à comprendre le pourquoi d’un ratage. Les progrès ne viennent en réalité que de l’accumulation d’échecs compris et surmontés. Les indications portées sur la fiche, détail des émaux et emplacement dans le four, vous permettront de tirer un maximum d’enseignements sur le travail des glaçures, la conduite de la cuisson et le comportement du four.
Un examen attentif des pièces au défournement vous permettra de faire l’apprentissage des principaux défauts des glaçures qu’il faudra essayer de corriger.
Un des plus graves est sans aucun doute la sur-cuisson ou l’excès de fusibilité de votre émail qui entraînera des coulures et collera votre pièce à la plaque d’enfournement. Il se peut qu’il y ait des différences importantes de température entre différentes parties du four et que le problème ne se pose que dans la zone la plus chaude. Sinon, la composition de l’émail ne convient pas pour la température choisie et il faudra la corriger en la «durcissant» un peu.
Le problème inverse est la sous-cuisson de l’émail qui est évidente par l’aspect sec et infondu de celui-ci. Là, le remède sera opposé au précédent.
Le tressaillage et son réseau de craquelures n’est vraiment un défaut que dans les basses températures quand il entraîne la porosité de la céramique. A haute température, ce peut-être aussi un choix esthétique et dans ce cas on ne parle plus de tressaillage mais de «craquelé». On peut même le rendre plus apparent en passant à froid sur l’émail de l’encre de chine. Ce phénomène est dû à la dilatation de l’émail supérieure à la dilatation de l’argile. A température de fusion de l’émail, l’accord avec l’argile se fait sans problème. C’est au refroidissement quand l’émail se fige que le phénomène se produit. Ne pouvant continuer à se contracter au-delà de la contraction de l’argile, la pellicule d’émail se fend en un réseau plus ou moins serré suivant que le désaccord émail/argile est plus ou moins important.
Le phénomène inverse est bien plus grave et ce défaut est appelé écaillage. Si l’argile se contracte davantage que l’émail, celui-ci peut effectivement se détacher par plaques, parfois entraîner la cassure de la pièce. Quand le phénomène est léger, il peut ressembler au tressaillage, le réseau apparaissant en clair sur l’émail. En passant le doigt on doit pouvoir sentir un léger dénivelé à la surface de l’émail. Il y a deux façons de corriger ce défaut, soit en modifiant la composition de l’émail, soit en modifiant celle de l’argile.
A la surface de l’émail apparaissent parfois des petits cratères, des trous gros comme des «têtes d’épingle» ou même des bulles. Ces défauts sont toujours dus à des dégagements gazeux qui laissent trace de leur passage dans les glaçures qui ont une grande viscosité. Une matière première légèrement hydratée comme le talc a une déshydratation très tardive. Elle se produit entre 890 et 1030 °C. A cette température, certaines glaçures rentrent déjà en phase pâteuse et piègent donc cette vapeur qui provoque le bullage. Pour comparaison, la déshydratation d’un kaolin se fait entre 430 et 780 °C. On peut résoudre le problème en calcinant son talc en four de dégourdi, en lui ôtant ainsi l’essentiel de son eau de constitution. Un palier en fin de cuisson peut aussi améliorer le nappage de l’émail.
On peut enfin tenter une recuisson pour une pièce «bullée» et Daniel de Montmollin me disait recuire parfois des émaux à «gouttes d’huile» dans une seconde cuisson réductrice pour obtenir un meilleur nappé sans rien perdre du décor de la première cuisson.
Enfin, je voudrais parler des problèmes de retirement. Certaines glaçures ont une tension superficielle très forte qui s’oppose à la formation de la couche intermédiaire et provoque un phénomène de contraction qui laisse une partie du tesson non émaillée. Là, il existe une image qui sera plus parlante qu’une longue démonstration : l’émail se comporte de la même façon qu’une goutte d’eau sur une surface grasse, incapable de mouiller la surface. Le phénomène apparaît dans les glaçures fortement dosées en silice et alumine et il est très visible dans l’angle supérieur droit de certaines plaquettes à 36 essais réalisées par le dosage en gouttes.
Une fois les pièces et les essais étudiés, j’archive désormais les résultats intéressants en photographies numériques. Pour chaque pièce, je conserve toutes indications sur l’émaillage, l’atmosphère de cuisson et l’emplacement dans le four.
C’est en effet une bibliographie sommaire car le sujet est bien trop vaste. Je vous indiquerai quelques vieux ouvrages de technologie céramique parus en gros entre le milieu du xixe et le milieu du xxe siècle. Ils sont difficiles à trouver et souvent onéreux mais il est possible de tomber sur la bonne affaire sur l’immense marché Internet, alors ne la ratez pas.
Je propose ensuite des ouvrages plus récents dans lesquels on trouvera des informations sur les émaux de haute température. Je laisse volontairement de côté la littérature anglo-saxonne pourtant très riche.
Enfin, je conseillerai également quelques livres qui vous permettront de connaître l’œuvre de grands céramistes. Vous y trouverez sûrement matière à réflexion et sources d’inspiration.
8 chemin des Fourches — 93380 Pierrefitte-sur-Seine. Tél. : 01 48 23 75 34.
61 rue marconi, B.P. 3 — 62880 Vendin-le-Vieil. Tél. : 03 21 79 44 44.
Son site Internet : http://www.revue-ceramique-verre.com
Les techniques sont rarement abordées dans la revue de la céramique et du verre. Il existe cependant quelques articles qui vous apporteront des informations sur les émaux de haute température ; en voici les références. Sachez qu’il est possible de retrouver sur un DVD l’intégralité des anciens numéros, du n°1 au n°145 :
Ce document a été traduit de LATEX par HEVEA